- #1
Caution
- 9
- 0
Homework Statement
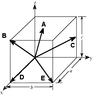
Identify the [221] vector?
A
B
C
D
E
Homework Equations
The Attempt at a Solution
I reduce [221] to [1 1 0.5].BUT after getting the wrong answer, the feed back is as follows
"Feedback: [221]: has a 0.5 component along the x-axis; a 0.5 component along the y-axis and a 1 component along the z-axis.
Why is it[0.5 0.5 1]? And even so i can't seem to find the answer from the choices.. Pls help (I jus started this module.)