Tiago3434
Homework Statement
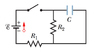
In Fig. 27-66, R1= 10.0 kΩ, R2 = 15.0 kΩ, C = 0.400 µF, and the ideal battery has emf E = 20.0 V. First, the switch is closed a long time so that the steady state is reached. Then the switch is opened at time t = 0. What is the current in resistor 2 at t = 4.00 ms?
This is question 8 of the following pdf if you need the picture (I don´t have a clue about how to include a picture in the question)
http://www.phys.ufl.edu/~majewski/2049/solns/hw5/hw5_solutions.pdf
It´s also question 65 of chapter 27 of Halliday
Homework Equations
The Attempt at a Solution
I understand the solution the way it´s done through the voltage drop across the capacitor being the same as through resistor 2, but I don´t get why couldn´t i just find the current in the circuit at time t=4ms, given that all the charge in one of the plates passes through resistor 2? I know this method right here is wrong, because it yields a different answer, but could someone tell me why?