RelativeJosef
- 6
- 1
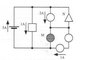
Homework Statement
Find currents through M and N
Homework Equations
Current out must be current in.
The Attempt at a Solution
I think that it is simply 3 parallels running with 5A of current. So, M is in series with the 2A current thus also has 2A of current. Would N also be in series with the two elements with 1A of current, thus making it's current also 1A?
I am confused because of the third pathway between the second and third parallel. Would the current try to skip the path with two elements in the bottom right?
So I think I am certain M has 2A of current. Then the question remains, Does N have 2A of current, or does the current run through all three elements in the third parallel making it's current 1A?