Cylinder balancing in a single plane and in two planes

[crinoid]

Homework Statement

Hollow cylinder balancing

Relevant Equations

F=m·r·(ang_v)^2
T=F·l

Homework Statement: Hollow cylinder balancing
Homework Equations: F=m·r·(ang_v)^2
T=F·l

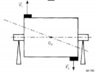
Hi, I want to know how the hollowness of a cylinder would affect its balancing process.
A little introduction: There are 2 different types of balancing: in a single plane (static balance) and in 2 planes (dynamic balance). The first one is intended for disk-like objects and the second one is for rod-like ones (the axis dimension, L, is not negligible in relation to the diameter D).
I have a guideline stating the type of balancing process needed according to the L/D ratio and the angular velocity [rpm]. The problem is that the guideline is intended for "filled" cylinders, not hollow ones.
Do you think that the hollowness would make the cylinder more disk-like or do you think I does not affect? What I've tried so far:
Inertial force: F=m·r·(ang_v)^2 --- m: unbalance mass; r: radius (mass imbalance, U=m·r)
Torque: T=F·l; --- l: distance between the forces
Force in each support: Fs=F·(l/h) --- h: distance between supports
In the worst case scenario: Fs=U*ang_v^2*L/h
According to ISO 1940/1, there is an acceptable maximum mass imbalance for each kind of machine, defined by each quality grade G: G[mm/s]=U·ang_v/m_rotor, so U<G·m_rotor/ang_v
I don't know how could I relate this to the shape of the rotor

Thanks in advance
Adrián

Ps: Sorry for my English, it's not my native tongue

 

[haruspex]

I don't know how could I relate this to the shape of the rotor

Since the case you are interested in is a rod-like axle, it isn't going to make much difference whether it is hollow or solid.
However, I do not know how the expression for G is arrived at.