FallenApple
- 564
- 61
Ok so we all know that when rolling down a fixed incline under gravity, a sphere will beat a cylinder in a race due to the fact that it has less rotational inertia.
However, in the following set up, the cylinder beats the sphere.
Say the cylinder and sphere are side by side on a horizontal plank. The plank is pulled such that the sphere and cylinder rolls on it without slipping. Say that the plank is pulled to the right.( diagram below). We want to know in a race to the right, which would win. In the lab frame of reference, both the objects would be accelerating linearly forwards to the right( because of friction) while in the plank from of reference, both objects would be accelerating to the left.
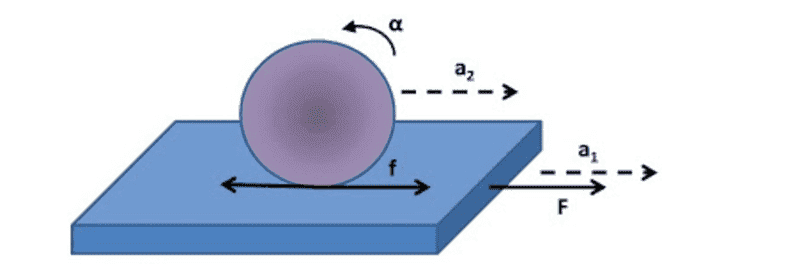In the diagram, for a rolling object in general, a1 is the planks acceleration relative to the lab frame and a2 is the linear acceleration of the rolling object relative to the lab frame.
According to my calculations, the linear acceleration of the cylinder is 1/3=.33 of the acceleration of the plank while the linear acceleration of the sphere is 2/7=.29.
So if they start side by side, and we pull the plank to the right for 1 sec. Then the cylinder would have traveled about .33 meters to the right while the sphere would have traveled about .29 meters to the right, making the cylinder win.
But that was just from a calculation and not that satisfying for developing intuition.
So would the following reasoning work?
If I want to know which one wins, I don't need to do any calculations other than knowing the moments of inertia of the sphere and cylinder.
When the plank accelerates to the right, for both objects to be rolling without slipping, they must roll counterclockwise. In the reference frame of the plank, both are rolling to the left, with a ficticious force acting on their CMs, pulling them to the left, opposing friction. So since this is like the incline problem above. The sphere's smaller moment of inertia would give less resistance to rolling, hence less resistance to the left acceleration under the ficticious force, hence in the plank frame, the sphere wins, as expected. But in the outside lab frame, this means that the sphere stays more left than the cylinder over time.
Does this reasoning work?
What about the lab frame? Can I say from the lab frames perspective the one with the higher moment of inertia (the cylinder) would not like to have as much angular acceleration, so most of it's motion is in it forward linear acceleration as compared to the sphere, where the ratio of its forward linear acceleration to its angular acceleration would be less.
However, in the following set up, the cylinder beats the sphere.
Say the cylinder and sphere are side by side on a horizontal plank. The plank is pulled such that the sphere and cylinder rolls on it without slipping. Say that the plank is pulled to the right.( diagram below). We want to know in a race to the right, which would win. In the lab frame of reference, both the objects would be accelerating linearly forwards to the right( because of friction) while in the plank from of reference, both objects would be accelerating to the left.
According to my calculations, the linear acceleration of the cylinder is 1/3=.33 of the acceleration of the plank while the linear acceleration of the sphere is 2/7=.29.
So if they start side by side, and we pull the plank to the right for 1 sec. Then the cylinder would have traveled about .33 meters to the right while the sphere would have traveled about .29 meters to the right, making the cylinder win.
But that was just from a calculation and not that satisfying for developing intuition.
So would the following reasoning work?
If I want to know which one wins, I don't need to do any calculations other than knowing the moments of inertia of the sphere and cylinder.
When the plank accelerates to the right, for both objects to be rolling without slipping, they must roll counterclockwise. In the reference frame of the plank, both are rolling to the left, with a ficticious force acting on their CMs, pulling them to the left, opposing friction. So since this is like the incline problem above. The sphere's smaller moment of inertia would give less resistance to rolling, hence less resistance to the left acceleration under the ficticious force, hence in the plank frame, the sphere wins, as expected. But in the outside lab frame, this means that the sphere stays more left than the cylinder over time.
Does this reasoning work?
What about the lab frame? Can I say from the lab frames perspective the one with the higher moment of inertia (the cylinder) would not like to have as much angular acceleration, so most of it's motion is in it forward linear acceleration as compared to the sphere, where the ratio of its forward linear acceleration to its angular acceleration would be less.