Cylindrical conductor with an off center cavity

[arunma]

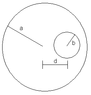
I have a quick question. I recently did an E&M problem in which I was given a cylindrical conducting wire of radius a, in which someone bores an off-center cylindrical cavity of radius b (the center of the smaller circle is offset from the center of the wire by distance d). I'm asked to find the magnetic field inside the cavity. I've attached a crude diagram to illustrate the problem. Anyway, I understand how to do the solution: find the magnetic field of a normal cylindrical wire, superimpose another wire with current flowing in the opposite direction, where the cavity is supposed to be, and then add the magnetic fields. And of course there's a simple coordinate transformation involved.

There's just one part of this solution that I don't understand. When calculating the magnetic field from the larger wire by using Ampere's Law, it's necessary to find the current density. I assumed that it would be J = \dfrac{I}{\pi a^2}. But it turns out that I need to subtract off the area of the smaller circle, so that J = \dfrac{I}{\pi (a^2-b^2)}. Can anyone explain qualitatively why this is necessary? I thought the cavity was already accounted for by superimposing the current in the other direction.

 

[Doc Al]

I assumed that it would be J = \dfrac{I}{\pi a^2}.

That assumes that the current through the wire is uniformly distributed over the full area--but it's not, since there's a hole!

But it turns out that I need to subtract off the area of the smaller circle, so that J = \dfrac{I}{\pi (a^2-b^2)}. Can anyone explain qualitatively why this is necessary?

The current that would have gone through the part of the wire where the cavity is must instead go through the rest of the area--increasing the current density. (Current only flows where the wire actually is. )

I thought the cavity was already accounted for by superimposing the current in the other direction.

Right, but only if you use the correct current density.

 

[arunma]

Well...that sort of makes sense. Thanks Al!