gkamal
- 36
- 0
1. Homework Statement
A DC circuit is shown below. Note the ground (V=0) in the circuit
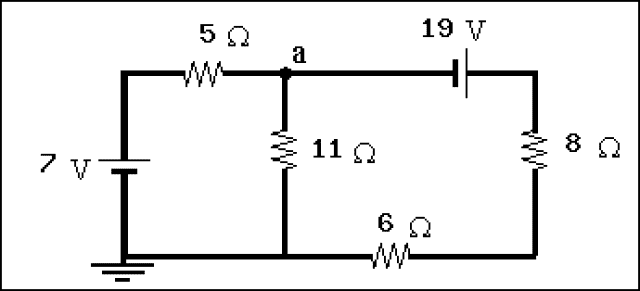
1- calculate the current through the 5Ω resistance. Use "+" sign for the current directed from right to left, and "-" sign if the current flows from left to right.
2- The sign of the potential at a is:
3- The magnitude of the potential at a is:
I1=I2+I3
-11I2+7-5I1=0
19-8I3-6I3+7-5I1=0
I1 being the current flowing clockwise in the loop from 7V going down [a] and back to 7V
I2 being the current going down [a] through the 11ohm resistor
I3 is the loop going anti-clockwise from 19V up the 11ohm resistor and back to 19 V
3. Attempt at solution :
I found the answer for number 1 to be 1.12 A but I am not sure if its right and not sure what is the sign for the direction.Also, i found the answer for number 2 to be positive but I do not understand it fully so please explain , for number 3 I have no clue what to do
A DC circuit is shown below. Note the ground (V=0) in the circuit
1- calculate the current through the 5Ω resistance. Use "+" sign for the current directed from right to left, and "-" sign if the current flows from left to right.
2- The sign of the potential at a is:
3- The magnitude of the potential at a is:
Homework Equations
I1=I2+I3
-11I2+7-5I1=0
19-8I3-6I3+7-5I1=0
I1 being the current flowing clockwise in the loop from 7V going down [a] and back to 7V
I2 being the current going down [a] through the 11ohm resistor
I3 is the loop going anti-clockwise from 19V up the 11ohm resistor and back to 19 V
3. Attempt at solution :
I found the answer for number 1 to be 1.12 A but I am not sure if its right and not sure what is the sign for the direction.Also, i found the answer for number 2 to be positive but I do not understand it fully so please explain , for number 3 I have no clue what to do
Last edited: