DC Circuits Question (internal resistance)

[KierstenKudos]

Homework Statement

Determine the magnitudes and directions of the currents through R1 and R2 in Fig. 19-47, where R1 = 37 and R2 = 16 .

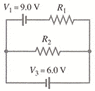
Figure 19-47
(image attached)

V1 = 9.0 V
V3 = 6.0 V
R1 = 37 \Omega
R2 = 16 \Omega

Homework Equations

V = IR

The Attempt at a Solution

V = IR
6.0 V = (37\Omega) I
.16216 A = I _{}1(correct)

V = IR
6.0 = (16\Omega) I
.375 A = I_{}2 (incorrect)

 

[Redbelly98]

The Attempt at a Solution

V = IR
6.0 V = (37\Omega) I
.16216 A = I _{}1(correct)

V = IR
6.0 = (16\Omega) I
.375 A = I_{}2 (incorrect)

That's weird, I would say I1 is incorrect and I2 is correct. Did you get the 16Ω and 37Ω values reversed perhaps?

Kirchof's Voltage Law (KVL) would be useful here.