Defining which cyclist profits the most from slipstream

[Physicsterian]

Homework Statement

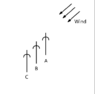
- Question: Which cyclist (A, B or C) profits the most from cyclist slipstream (also called “aerodynamic drafting”)?
- Given: the direction of the wind, the positions of each cyclist; an illustration representing this
- NOTE that I am expected to solve this question conceptually, without using a pen, paper and/or calculator. From personal interest, however, I am also wondering if the problem could be solved concretely. However, the priority right now is, solving it conceptually.

Homework Equations

- Perhaps, the drag reduction due to slipstream could be estimated(/calculated) by using the drag equation, which is FD = ½ ρ * v^2 * Cd * A (with FD = Drag force, ρ = fluid density, v = Relative velocity between the fluid and the object, Cd = Drag coefficient and A = Transversal area or cross sectional area)

The Attempt at a Solution

According to the answer sheet, confusingly enough, the answer is cyclist B. What I can make up from the situation is that cyclist A catches up a significant amount of the oncoming wind force, which favors cyclist B in that he or she has to put in less effort against the wind force. The x as well as y component of the wind force are reduced, meaning that the "v^2" in "FD" and thus "FD" becomes smaller. So far, so clear. However, I do not get it why it is not cyclist C who profits the most of drag-reduction, as cyclist B catches up a great amount of the wind that passes by cyclist A, wherefore C should face the oncoming wind even less than B. Wondering what I am doing wrong. The only reason I can think of is the fact there are three arrows and that that might be explanatory for B profiting more from slipstream compared to C, but I fail to make a logical conclusion.

Might something not be clear enough, please let me know.
Thanks a lot in advance.

 

[CWatters]

Perhaps think what happens to the airflow behind a solo cyclist. What happens to the airflow behind you if there is someone close behind you?

 

[Physicsterian]

https://www.physicsforums.com/attachments/230252

Perhaps think what happens to the airflow behind a solo cyclist. What happens to the airflow behind you if there is someone close behind you?

Firstly, thank you for the directions.

Behind each solo cyclist a low pressure wake can be expected (I guess this can be referred to as “leeward pressure”, see picture). And if someone is slightly sideways close behind a cyclist, he does not only profit from the slipstream of the cyclist in front of him, but also presses air towards the cyclist in front of him.

However, at the other hand, I can also think of a disruption of laminar airflow, a.k.a. turbulent flow, and in the worst scenario, vortices behind cyclists, which would, I think, have a negative impact on a cyclist that is being straight behind.

Now, trying to relate this to why cyclist b should profit more from the slipstream / drag reduction, I arrive at the following assumption: the extent to which cyclist B profits from cyclist A's slipstream and the forward acting pressure caused by C, must be greater than the friction caused by the disrupted airflow behind A. Whereas, C will be subject to the disrupted airflow created by both A and B and won't have a cyclist behind him pushing air forward on him. So, I think that the effect of the airflow disruption and the absence of air pushing from behind must be stronger than the drag reduction created by A's and B's slipstream.

Am I somewhat on the right track?

 

[berkeman]

Whereas, C will be subject to the disrupted airflow created by both A and B and won't have a cyclist behind him pushing air forward on him.

Air does not get "pushed" onto the rider in front of you when you are drafting...

Think also about what happens in swimming workouts and open-water swimming races. Swimmers draft much like cyclists do. As both a cyclist and a swimmer, I know which one of those three positions I'd want to be in...

 

[Physicsterian]

Think also about what happens in swimming workouts and open-water swimming races. Swimmers draft much like cyclists do. As both a cyclist and a swimmer, I know which one of those three positions I'd want to be in...

Good to know that swimmers also practice drafting. I have been searching on the web using different terms and found out several facts related to my question. Firstly, that it is indeed best to draft immediately behind a swimmer, instead of at the so called hip-position (http://www.220triathlon.com/training/swim/how-much-time-does-drafting-save-when-swimming/10378.html). I learned that wake is actually a disturbed flow of fluid / recirculation of fluid caused by the fluid moving around the body of the swimmer. The same is also applicable to aircraft and the effect is way stronger for air. The reason of wake seems to lie in viscosity, and it often seems to go along with flow separation. I read, that when the flow is massively separated, a reverse flow region is induced behind the body where the fluid is moving back toward the swimmer/aircraft. It seems to me that, that is the phenomena that causes the slipstream / drag reduction that the person/vehicle experiences... Most logically, the slow down of the fluid at the back of the vehicle due to viscosity and the low pressure area created should be the factors responsible for reducing drag behind there. However, the cyclists are not positioned directly behind, but rather more leftward-behind, so I have difficulties with concluding if the same applies then, and if so, how. And the last thing I fail to understand is, how the wind (which comes from northeastward toward the cyclists) effects the amount of slipstream each cyclist experiences and why cyclist B is more in favor compared to C. My logic tells me that C should be more in favor as it is more "protected" against the wind.

And one more thing that creates a contra-feeling, is that the disturbance of air in wake regions, must produce drag, which should be in disadvantage of the person/vehicle behind. It is even known that vortices of aircraft are extremely dangerous for the aircraft flying behind and thus should be avoided.

The last piece of info related to the subject I found that might be helpful is that birds use a similar method when flying in a v-flight; in that case the birds manage to reduce the downward acting weight force by making use of the updraft created by the front bird's flying (https://en.wikipedia.org/wiki/V_formation).

I found a lot of info, yet can't manage to give a concrete answer to my topic question. Might I be confusing different terms or am I maybe relating them wrongly.
Hopefully, you can direct me through this, I really wonder about your valuable opinions

Thanks a lot in advance.

 

[haruspex]

Air does not get "pushed" onto the rider in front of you when you are drafting...

Well, perhaps not precisely so, but I believe the rider behind will aid the one in front.
Compare being in the middle of an entire pack with being at the back. The first would be like riding inside a car while the second is like being right behind it, where there would still be some drag.

 

[Physicsterian]

I just found this picture, which is an explainer for how drafting works for cars. Its clear to me that the vehicle in the middle profits the most from draft. Do you believe the same principle will work in the case of the diagonally arranged bikes (see uppermost post) which are traveling not entirely head to tail as depicted above? If so, what is the explanation for it? I tried to draw out the direction of the airflow and its effects on the bikes - see attachment - but after research using several terms and visualization of the situation, I still don't manage to see why bicycle B should benefit more from slipstream. Hope someone can provide directions.

 

[berkeman]

I just found this picture, which is an explainer for how drafting works for cars. Its clear to me that the vehicle in the middle profits the most from draft.

That picture and airflow are for streamlined cars going 150mph+ with specific body shapes. IMO, that does not apply to bicycle riding or racing.

Well, perhaps not precisely so, but I believe the rider behind will aid the one in front.

I've never felt any benefit to having a rider behind me. Other than the psychological motivation to keep pedaling hard!

Have a look at how line riding works in cycling. When you have a line of riders, when the lead rider gets a little tired, he or she peels off and slows a bit to let the line pass and joins in at the back of the line. If it were easier to be in the #2 position, bicycle racing strategies would be completely different from what they really are now...

 

[haruspex]

If it were easier to be in the #2 position, bicycle racing strategies would be completely different from what they really are now...

I don't see why. Everyone gets a turn in every position.

Cycling Skills: Most efficient positions in a pack
10 Jul 2008 · But as you get to the back of the pack, in the line of single-file riders trailing the peloton, you actually start to get less draft. Repeat: further back does not always mean an easier ride—you can sit too ...

Also:
https://www.hpcwire.com/2018/07/05/...veals-best-position-in-a-peloton-of-cyclists/

Though whether these results apply to a mere trio of riders is unclear.

 

[berkeman]

Looks like Google says I'm right about being farther back in the pace line having more advantage (even though I'm wrong that the lead rider gets no benefit -- but the 2nd rider has to overlap wheels for the front rider to get this benefit, too scary for me and my riding buddies!).

First hit on the list of a Google search for Bicycle Drafting: https://www.bicycling.com/training/a20026446/how-to-draft/

Leader's Bonus
Pulling is not a thankless job. The first cyclist enjoys up to a 3.1 percent reduction in wind resistance courtesy of a low-pressure air bubble between riders, which pushes the leader along, says Bert Blocken, PhD, professor of physics at the Eindhoven University of Technology in the Netherlands, who led some of the research. Keep a steady pace on the front to avoid surging away from the boost—and splintering the group.

Stay Close
To get the maximum benefit in a paceline, keep your wheel as close as possible to the one in front of you. Ideally, ride in a staggered position with your front wheel just overlapping the rear wheel of the rider ahead of you. If you're not okay with taking that risk, don't worry—you can be as far back as about 3/4 of a wheel length and still save some energy.

Sweet Spot
The benefit of drafting gradually increases from the second rider to the fifth before starting to level off. In groups up to five, the last rider enjoys the most aerodynamic benefit, Blocken says. But in a group of six to eight (roughly the number in a team time trial), the next-to-last position feels the least wind resistance. In a big, hard-charging pack, the best position is between fifth and eighth. You get a large aero benefit, Blocken says, and you're less likely to get into a crash.

EDIT -- I didn't see the links by @haruspex before I posted my link. Not sure if they agree or disagree...

 

[Physicsterian]

https://www.hpcwire.com/2018/07/05/...veals-best-position-in-a-peloton-of-cyclists/
Though whether these results apply to a mere trio of riders is unclear.

Yes, that's what I was referring to with my "pushing air" statement.

After having seen the peleton formation, I don't really think the results will apply to a mere trio, as the formation is basically too small and there are no shelter providing cyclists at the right, making the peleton have different characteristics compared to a v-shaped one.

@berkeman

"The benefit of drafting gradually increases from the second rider to the fifth before starting to level off. In groups up to five, the last rider enjoys the most aerodynamic benefit, Blocken says. But in a group of six to eight (roughly the number in a team time trial), the next-to-last position feels the least wind resistance."

In the mean time, I looked up how line riding works, and came across Echeloning, which looks identical to the situation illustrated in my topic picture. However, I could not find which of the cyclists in the back of the echelon benefits most. And I came across the same research of prof. Blocken. However, the situation there is a v-shaped peleton, whereas in my picture it is sort of half a peleton. What's your opinion; do you think the same effect will apply to echelon formations?

 

[haruspex]

do you think the same effect will apply to echelon formations?

The echelon is essentially the crosswind equivalent of the line formation. The main difference would be that the riders are effectively closer.

 

[Physicsterian]

The echelon is essentially the crosswind equivalent of the line formation. The main difference would be that the riders are effectively closer.

Got it. In the case of diagonally approaching crosswind, the "position" of the slipstream areas do change as the crosswind is disturbing it partly , doesn't it? Thus, shouldn't that mean, that the rules for defining which cyclist experiences the most slipstream, change in an echelon formation?

 

[berkeman]

Got it. In the case of diagonally approaching crosswind, the "position" of the slipstream areas do change as the crosswind is disturbing it partly , doesn't it? Thus, shouldn't that mean, that the rules for defining which cyclist experiences the most slipstream, change in an echelon formation?

In my experience, drafting is less effective when you are dealing with a quartering headwind. Even though you can get closer since you are in echelon formation, there is extra turbulence compared to straight line drafting.

@Physicsterian -- I want to commend you on doing so much research and reading trying to figure this problem out. Many students come here just to get answers without doing much reading. You have shown us that you are willing to follow our links and do your own searching to try to figure this non-trivial problem out. Well done!

I would be interested in the final answer from your instructor. I think if you submit all of your research and the potential answers from that reading, you should get full credit for your answer. I personally would still go for the 3rd rider having the easiest time, but based on some of the links, that answer is not a slam dunk. Please let's us know what you submit for the answer, and what the instructor feedback is.

 

[Physicsterian]

In my experience ... and what the instructor feedback is.

Thanks a lot! I think its proper ethic to do so if you expect guidance/help, so I do my best. I will absolutely go behind it and come back at it here.

I still doubt between the last and mid one, but after having slept a night over it, I think I GOT IT :) ! I feel more inclined towards the mid one. Why?: I have taken a new perspective on it: simply, interpreting that the crosswind, that attacks from aside, acts in the same way as the wind that acts from the front: it creates drag. That means that, similarly, a sort of (how shall we call it) "sideward" vacuum-effect will be created over the one in the middle. And, even though, their still is a y component of the crosswind that will attack each cyclists from the front, the mid-one will benefit the most from the slipstream created by the x-component of the crosswind. The last one will - exactly such as in the car illustration I attached above - experience less slipstream. (I think that, in this particular case, the leftmost one must be seen as a kind of "semi-gutter"). Also, looking at the v-formation of prof. Blocken, it looks like my assumption finds its place; the ones in the middle must be most protected, because of what I just described regarding the x and y component of the wind. At least, that's what I can think of and seems most logical to me...

 

[Ekooing]

I'm not sure if anyone has given the answer you're looking for, but in case not, let me give it a shot. If there were just one cyclist, they would have to cycle against both the air they are hitting by going forward, and from a low pressure that forms behind them that tries to "pull" them back. The second cyclist in line wouldn't have as much of that negative pressure behind them because the third cyclist would be riding in the slip stream of cyclist B, and therefore would "break up" the air flow behind cyclist B. So cyclist A is pushing against the wind, and cyclist C has the negative pressure behind them "pulling" them back. Cyclist B wouldn't have either (or would at least have less of both forces).

 

[berkeman]

I'm not sure if anyone has given the answer you're looking for, but in case not, let me give it a shot. If there were just one cyclist, they would have to cycle against both the air they are hitting by going forward, and from a low pressure that forms behind them that tries to "pull" them back. The second cyclist in line wouldn't have as much of that negative pressure behind them because the third cyclist would be riding in the slip stream of cyclist B, and therefore would "break up" the air flow behind cyclist B. So cyclist A is pushing against the wind, and cyclist C has the negative pressure behind them "pulling" them back. Cyclist B wouldn't have either (or would at least have less of both forces).

Welcome to the PF.

As you hopefully have noticed, here at the PF we post links to reputable information sources when making assertions. Please post the links to the information you researched when forming your reply. Your reply is not necessarily bad, but making unsupported assertions is not generally allowed here.

If you are a pro bicycle racer offering your insights, that would be different. Otherwise, please read all of the links that have been posted so far, and add in your helpful links to the discussion. Thanks.

 

[Ekooing]

I'm a chemical engineer who took 3 years of physics in college, I tutor a high school student in physics, and this basic phenomenon is covered in high school physics. I didn't look it up necessarily, just like I wouldn't look up an answer if someone asked "what causes the tides in the ocean". I can find a high school physics book to reference if I need to provide a source though. Just let me know if I should do that.

Thanks,
Charles

 

[Ekooing]

Welcome to the PF.

As you hopefully have noticed, here at the PF we post links to reputable information sources when making assertions. Please post the links to the information you researched when forming your reply. Your reply is not necessarily bad, but making unsupported assertions is not generally allowed here.

If you are a pro bicycle racer offering your insights, that would be different. Otherwise, please read all of the links that have been posted so far, and add in your helpful links to the discussion. Thanks.

Sorry, I am knew to the forum as you pointed out, so I didn't know if I needed to quote your post first in order for you to see my response. In case that is the case, here it is again:

I'm a chemical engineer who took 3 years of physics in college, I tutor a high school student in physics, and this basic phenomenon is covered in high school physics. I didn't look it up necessarily, just like I wouldn't look up an answer if someone asked "what causes the tides in the ocean". I can find a high school physics book to reference if I need to provide a source though. Just let me know if I should do that.

 

[haruspex]

I didn't look it up necessarily

If you read through the earlier responses in the thread you will see that neither the theory nor practice support the view that the middle of a long line is the optimum position. Rather, it is towards, but not at, the rear. This makes it an open question as to which of second and third is best of three. Hence @berkeman 's request for a link supporting your statements.
This is rather different from a well-settled question such as the cause of tides.

 

[Ekooing]

If you read through the earlier responses in the thread you will see that neither the theory nor practice support the view that the middle of a long line is the optimum position. Rather, it is towards, but not at, the rear. This makes it an open question as to which of second and third is best of three. Hence @berkeman 's request for a link supporting your statements.
This is rather different from a well-settled question such as the cause of tides.

I was talking about the theory behind my answer. It is the same concept that causes drag on airplane wings (the vortex shedding that occurs on the trailing edge of the wing). If there were another wing directly behind the first one, the comparatively laminar flow that occurs when the air travels over the wing could continue off of the first wing and over the second one before the vortex shedding occurred. This would transfer the drag effect to the second wing. The same concept can be applied to a cyclist as vortex shedding can occur at those lower speeds.

I thought the OP stated that the answer was cyclist "B" and he was asking why. Perhaps misread his statement, but I was simply trying to provide a possible solution that was rooted in physics. Again, I can provide references that explain this phenomenon if that might help people understand it better. I just figured, based on the terminology that most people who have responded have used, that most of the somewhat basic physics concepts were already understood by most here. That's the only reason I didn't provide a reference in the beginning. But I will try to see if I can easily find something online that I can provide a link to that would explain the effect better than I can.

 

[Ekooing]

If you read through the earlier responses in the thread you will see that neither the theory nor practice support the view that the middle of a long line is the optimum position. Rather, it is towards, but not at, the rear. This makes it an open question as to which of second and third is best of three. Hence @berkeman 's request for a link supporting your statements.
This is rather different from a well-settled question such as the cause of tides.

I just reread OP's initial question and he/she did indeed say that the answer sheet said the correct answer is cyclist "B". Since OP made this assertion, I was simply trying to provide a reasoning why this may have been the correct answer.

 

[Physicsterian]

I'm not sure if anyone has given the answer you're looking for, but in case not, let me give it a shot. If there were just one cyclist, they would have to cycle against both the air they are hitting by going forward, and from a low pressure that forms behind them that tries to "pull" them back. The second cyclist in line wouldn't have as much of that negative pressure behind them because the third cyclist would be riding in the slip stream of cyclist B, and therefore would "break up" the air flow behind cyclist B. So cyclist A is pushing against the wind, and cyclist C has the negative pressure behind them "pulling" them back. Cyclist B wouldn't have either (or would at least have less of both forces).

Firstly, hi and welcome! Thank you for your input, every new view helps me in strengthening my general look at the subject, thus I am thankful for it.

I had come across the same theory for in-line constructions. However, I really wonder about whether or not the same of what you described is applicable to the Echelon setting with crosswind being present (?). Berkeman, Haruspex and Cwatters have put a lot of effort in helping me, and we indeed arrived at some important conclusions. However, because of the practical complicatedness of the matter, I think we all still have some doubts to a certain extent. Curious what your view is on the Echolon setting. I trust you on your word and profession, and will search further based on the search terms I am able to filter out in order to find sources. Help by getting views is my priority; I rather hear a new view without a source, than that you keep it for yourself, because you can't find or don't have time to provide a source. However, might you find a source, it would be of awesome additional value of course.

 

[berkeman]

I'm a chemical engineer who took 3 years of physics in college, I tutor a high school student in physics, and this basic phenomenon is covered in high school physics. I didn't look it up necessarily, just like I wouldn't look up an answer if someone asked "what causes the tides in the ocean". I can find a high school physics book to reference if I need to provide a source though. Just let me know if I should do that.

As mentioned by @haruspex giving a simplistic answer may not apply in the case of this problem. Even though the stated answer was "B", that is only true under a limted set of circumstances (see the links we posted). It generally helps the student the best with problems like these to post links that lead to the research that has been done on the subject, so they can read and learn for themselves what the tradeoffs are. So the correct answer for this problem may well be "B", but that answer is best qualified by "under the following conditions...". It is certainly not true under all conditions, and is not true in my experience of riding thousands and thousands of miles on my bike.

You may well have a reasonable background to try to answer this question to help the OP. That's a good thing. But, especially since you are new here, we really have no way to know what your background is, and whether the points you were making are valid in the regions of airflow that would occur in this problem. That's why it's always a good thing to find some useful links at reputable sources and post those along with your analysis and thoughts. If you spend some more time reading the technical PF forums, you'll see this practice followed a lot, and it leads to interesting discussions where we all learn new things. I've certainly never felt any help by the rider drafting behind me, but as my link showed, there is a couple of percent gain for the lead rider, but only had higher speeds and only with overlapping wheel drafting.

Even true experts like the PF Science Advisor @boneh3ad (PhD in fluid mechanics and an Aero expert) generally post links to more information when answering questions. These topics are complicated enough that there are many conditions that need to be considered when discussion aerodynamics or other similar technical topics.

It's good to have you at the PF.

 

[256bits]

I was talking about the theory behind my answer. It is the same concept that causes drag on airplane wings (the vortex shedding that occurs on the trailing edge of the wing). If there were another wing directly behind the first one, the comparatively laminar flow that occurs when the air travels over the wing could continue off of the first wing and over the second one before the vortex shedding occurred. This would transfer the drag effect to the second wing. The same concept can be applied to a cyclist as vortex shedding can occur at those lower speeds.

The "problem" with this problem is that there is no indication as to what speed the cyclists are travelling.
All we know is that there is a crosswind of some sort.
In the diagram of riders and wind, is the absolute velocity of the crosswind represented, or the airspeed that the riders experience?
As @berkeman stated, an explanation may be true under certain conditions, while not under others.
Since the diagram does not give forward speed for the riders, one could even consider that they are at the beginning of the race, standing still, awaiting the starter pistol to commence the race, and have to lean into the wind, turning their front wheel, so as to not fall over. Which rider has the most, and which has the least discomfort in such a lineup?
Questions such as this beg for assumptions to be made, some off the cuff from intuition, some from experience, and some coming from a knowledge of the "equations." The vortex shedding explanation that you proposed led me to wonder if riders ever experience the Karman Vortex Street ( vortex alternating from side to side ), or would they ever know owing to action od pedaling. Some thing to think about, but I do doubt if it would ever be found in any literature on cycling.

 

[Ekooing]

The "problem" with this problem is that there is no indication as to what speed the cyclists are travelling.
All we know is that there is a crosswind of some sort.
In the diagram of riders and wind, is the absolute velocity of the crosswind represented, or the airspeed that the riders experience?
As @berkeman stated, an explanation may be true under certain conditions, while not under others.
Since the diagram does not give forward speed for the riders, one could even consider that they are at the beginning of the race, standing still, awaiting the starter pistol to commence the race, and have to lean into the wind, turning their front wheel, so as to not fall over. Which rider has the most, and which has the least discomfort in such a lineup?
Questions such as this beg for assumptions to be made, some off the cuff from intuition, some from experience, and some coming from a knowledge of the "equations." The vortex shedding explanation that you proposed led me to wonder if riders ever experience the Karman Vortex Street ( vortex alternating from side to side ), or would they ever know owing to action od pedaling. Some thing to think about, but I do doubt if it would ever be found in any literature on cycling.

I completely agree with you. The question leaves a lot to be desired. That is why I keep trying to explain that I was not trying to argue my point, or claim that my answer was definitely the correct one. I was simply offering a viable reason as to why the "correct" answer was "B". I keep getting people trying to shoot holes in my answer like "in a line of rides, the greatest benefit is actually towards the middle/back of the pack, not the true middle", and things like that. I am not trying to debate the pros and cons of the question, or the actual benefits one would experience while riding (versus theoretical ones), or anything like that. I am simply trying to provide a reasonable explanation as to why the correct answer is "B". So while all of the points everyone have made are valid, let me clarify by stating that I am making a few basic assumption, like the answer has to be A, B, or C, and can't be something like "B and a half", and the riders are moving at a constant velocity (acceleration = 0).

 

[Ekooing]

Firstly, hi and welcome! Thank you for your input, every new view helps me in strengthening my general look at the subject, thus I am thankful for it.

I had come across the same theory for in-line constructions. However, I really wonder about whether or not the same of what you described is applicable to the Echelon setting with crosswind being present (?). Berkeman, Haruspex and Cwatters have put a lot of effort in helping me, and we indeed arrived at some important conclusions. However, because of the practical complicatedness of the matter, I think we all still have some doubts to a certain extent. Curious what your view is on the Echolon setting. I trust you on your word and profession, and will search further based on the search terms I am able to filter out in order to find sources. Help by getting views is my priority; I rather hear a new view without a source, than that you keep it for yourself, because you can't find or don't have time to provide a source. However, might you find a source, it would be of awesome additional value of course.

Absolutely. As for the vortex shedding/drag created by pressure differential between air in front of and behind the rider, it is the same concept as the airfoil image and car example given in previous answers.

As for the stacked formation, the cross wind on each rider can be broken down into force vectors that would be down and to the left of the riders. How large in magnitude each of those vectors are is a factor of the direction (or more accurately, at what angle) the wind impacts them. However, regardless of the angle, there is some downward (in relation to the image posted, not downward toward the pavement) force. So the wind is going to impede their ability to traverse forward. Also, the vortices that are shed will come off on the back left side of the riders. So their staggered positioning will protect them better against the crosswind shown than an in line formation would.

 

[256bits]

I keep getting people trying to shoot holes in my answer

Well, I don't know about that.
I think it is more of a "Why do you think so, and can it be backed up by known theory."
PF people are a pretty smart bunch, and do tend to come to some sort of a solution by bickering back and forth in a nice way.

Consider this, at low Reynold's number, say 1,
the flow would be expected to follow each rider's and bike contour, so there is no benefit from either drifting position. The drag is due to skin friction as there is no separation of the flow. As we move towards increasing airspeed, the pressure drag becomes more dominant. Eddies form behind the object but tend to follow closely. With more airspeed, the eddies break off and flow downstream. And etc.

For a cylinder in an airflow we can follow this,
http://www-mdp.eng.cam.ac.uk/web/li...al_dvd_only/aero/fprops/introvisc/node11.html
Since a rider on a bike is not a cylinder but a conglomeration of shapes, that is just for illustration purposes.
And for one cylinder only.
Add a second, a third, or more, and the flow pattern changes.
Some symmetry arises with multiple riders - three is not enough.

I think the experimentalists have a one up upon the theorists for this problem.
Even then there seems to be some disagreement whether or not the leading rider benefits, at least inline, let alone in this configuration with drifting.

 

[Ekooing]

Well, I don't know about that.
I think it is more of a "Why do you think so, and can it be backed up by known theory."
PF people are a pretty smart bunch, and do tend to come to some sort of a solution by bickering back and forth in a nice way.

Consider this, at low Reynold's number, say 1,
the flow would be expected to follow each rider's and bike contour, so there is no benefit from either drifting position. The drag is due to skin friction as there is no separation of the flow. As we move towards increasing airspeed, the pressure drag becomes more dominant. Eddies form behind the object but tend to follow closely. With more airspeed, the eddies break off and flow downstream. And etc.

For a cylinder in an airflow we can follow this,
http://www-mdp.eng.cam.ac.uk/web/li...al_dvd_only/aero/fprops/introvisc/node11.html
Since a rider on a bike is not a cylinder but a conglomeration of shapes, that is just for illustration purposes.
And for one cylinder only.
Add a second, a third, or more, and the flow pattern changes.
Some symmetry arises with multiple riders - three is not enough.

I think the experimentalists have a one up upon the theorists for this problem.
Even then there seems to be some disagreement whether or not the leading rider benefits, at least inline, let alone in this configuration with drifting.

From the standpoint of a person who rides bikes, you're probably correct - there is little to no difference. From a physics standpoint, even at low speeds, there may be little difference, but there's almost assuredly not zero difference. Since this question was asked from a physics standpoint as opposed to a practically standpoint, I stand by my answer.

And even if you said it had almost zero benefit, you can at least say there's no way it could make position "B" worse than position "C". So if you're asking which one benefits the most, again, I stand by my answer.

 

[256bits]

there is little to no difference

I should point out
I said at low Reynold's number, the position matter's less, and as low as a Reynold's of 1, position is irrelevant.
As the airspeed increases, drifting does come into play.
Rider's and bikes in a real race would have a Reynold's >> 1

 

[boneh3ad]

Let me first point out that I am not satisfied by any of the links posted in this thread. Neither of the two most relevant ones (the HPCWire link and the Bicycling one) cite their sources (a DOI link to the referenced papers would be nice) and pop-sci interpretations of fluid dynamic phenomena are notoriously terrible, even when reading straight off the abstract or conclusions of an actual research paper.

My very first inclination when reading the prompt at the beginning of the thread was that the middle rider would get the most benefit, and the answer that has been closest to how I would have explained that so far was given by @Ekooing. The front rider has to do the work of deflecting the oncoming air and the third rider has to deal with the turbulent wake, while the middle rider gets to exist in a bubble between the two that will largely consist of air moving an pretty close to the same average speed as the group.

If you read through the earlier responses in the thread you will see that neither the theory nor practice support the view that the middle of a long line is the optimum position.

So, according to what I have typed above, I would argue that yes, theory does support the view that the middle rider gets the most benefit in the short line depicted in the problem. In a long line, the system will likely be more complicated and I'd be surprised if it was exactly in the middle. In this regard, I especially doubt that earlier bicycling.com link that states that the final rider gets the most benefit in groups of up to 5. This does not pass the smell test for a fluid mechanician, and I suspect that statement stems from a misreading of the source material by the writer of that article. However, it did not cite its sources so I cannot confirm.

The "problem" with this problem is that there is no indication as to what speed the cyclists are travelling. All we know is that there is a crosswind of some sort. In the diagram of riders and wind, is the absolute velocity of the crosswind represented, or the airspeed that the riders experience?

I disagree that this is a problem. As is common when drawing out fluids problems, if you simply assume the problem was drawn in the frame of reference of the riders, then the figure simply shows that the combination of headwind and crosswind produces a resultant wind in the same direction as the riders' formation. That's a really simple assumption and one that is common enough in fluids that it is entirely justified, in my opinion. I'd also argue that the actual velocity doesn't really matter much, because any reasonable cycling situation is not going to be in the realm of Stokes flow ($Re\leq 1$) and isn't going to be occurring at extremely high $Re$ either. In the middle of those two, the qualitative principles remain unchanged.

 

[Physicsterian]

Thanks a lot for your views and the nice explanations @256bits , @Ekooing and @boneh3ad

Tomorrow, I will read through the info provided with the link and try to gain some more knowledge on terms like "eddies" and "stokes flow and try to link it to answering my question, and come back it it here.

 

[Ekooing]

Let me first point out that I am not satisfied by any of the links posted in this thread. Neither of the two most relevant ones (the HPCWire link and the Bicycling one) cite their sources (a DOI link to the referenced papers would be nice) and pop-sci interpretations of fluid dynamic phenomena are notoriously terrible, even when reading straight off the abstract or conclusions of an actual research paper.

My very first inclination when reading the prompt at the beginning of the thread was that the middle rider would get the most benefit, and the answer that has been closest to how I would have explained that so far was given by @Ekooing. The front rider has to do the work of deflecting the oncoming air and the third rider has to deal with the turbulent wake, while the middle rider gets to exist in a bubble between the two that will largely consist of air moving an pretty close to the same average speed as the group.
So, according to what I have typed above, I would argue that yes, theory does support the view that the middle rider gets the most benefit in the short line depicted in the problem. In a long line, the system will likely be more complicated and I'd be surprised if it was exactly in the middle. In this regard, I especially doubt that earlier bicycling.com link that states that the final rider gets the most benefit in groups of up to 5. This does not pass the smell test for a fluid mechanician, and I suspect that statement stems from a misreading of the source material by the writer of that article. However, it did not cite its sources so I cannot confirm.
I disagree that this is a problem. As is common when drawing out fluids problems, if you simply assume the problem was drawn in the frame of reference of the riders, then the figure simply shows that the combination of headwind and crosswind produces a resultant wind in the same direction as the riders' formation. That's a really simple assumption and one that is common enough in fluids that it is entirely justified, in my opinion. I'd also argue that the actual velocity doesn't really matter much, because any reasonable cycling situation is not going to be in the realm of Stokes flow ($Re\leq 1$) and isn't going to be occurring at extremely high $Re$ either. In the middle of those two, the qualitative principles remain unchanged.

Thank you for commenting here @boneh3ad and confirming my ascertain. As the forum's scientific adviser, I figure everyone will respect your opinion. I tend not to delve too much into my background when I'm answering questions such as these online as I don't want to sound like I'm bragging. However, I have realized that in this forum, people want to know that the information you provide is coming from a reliable source, so I figured I'd let you know my background for future reference. As stated before, I received my degree in chemical engineering, and from there I worked in pump design (all fluid mechanics), then worked in the aerodynamics and materials science departments for NASA for several years. Lastly, I have quite a bit of experience in the oil and gas industry. I am also the fluid mechanics consultant for a start up company designing a chemical sniffer system detecting chemical components in the ppb range.

Again, I provide this information to you not to show off, but simply to provide you with my background so you know where the information I post comes from.

 

[haruspex]

a DOI link to the referenced papers would be nice

The bicycling.com reference quotes Bert Blocken. Following that leads to https://www.europhysicsnews.org/articles/epn/pdf/2013/01/epn2013-44-1p20.pdf.

 

[Physicsterian]

Thanks a lot for your views and the nice explanations @256bits , @Ekooing and @boneh3ad

Tomorrow, I will read through the info provided with the link and try to gain some more knowledge on terms like "eddies" and "stokes flow and try to link it to answering my question, and come back it it here.

I went through the info about the eddies, nice to have learned about that as well.
Its a difficult decision, considering all the info, but I think I will go for B as my final answer for the particular echelon setting with all the info I have been able to gather till now. Any of you, who is advising to still absolutely not choose for B?