tolove
- 164
- 1
I'm not entirely sure on the properties of limits, but this seems to work. Could someone look over this for me?
http://imgur.com/6zCHYo5
http://imgur.com/6zCHYo5
Definitions and properties of limits (handwriting attached)
- Thread starter tolove
- Start date
-
- Tags
- Definitions Limits Properties
Join the discussion
Registration is free. Ask a follow-up in this thread, or start your own.
3 replies · 2K views
Discussion
- 11,987
- 1,584
tolove said:I'm not entirely sure on the properties of limits, but this seems to work. Could someone look over this for me?
http://imgur.com/6zCHYo5
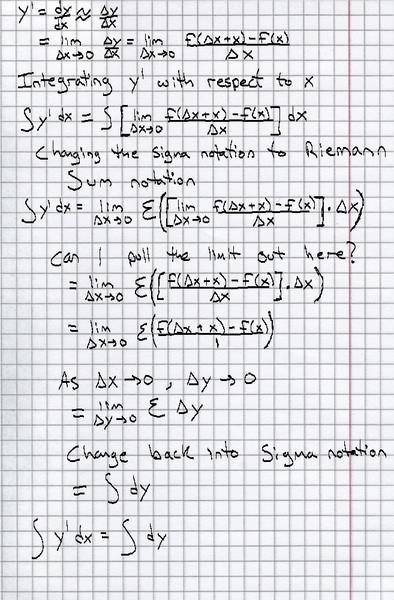
What is it that you're trying to do?
Please state the problem.
Attachments
tolove
- 164
- 1
SammyS said:
Not really a problem here, just wanting to make sure I'm doing this correctly. I'm trying to show that ∫ y' dx = ∫ dy through definitions.
- 11,987
- 1,584
tolove said:
What are you using for the definition of the indefinite integral?
The Riemann sum is generally used for the definite integral.