SuperCass
- 60
- 0
Deflection in a CRT, Potential Problem: Problem more than halfway solved, stuck
In Fig. 24-32 an electron is projected along the axis midway between the deflection plates of a cathode-ray tube with an initial speed of 6.40 106 m/s. The uniform electric field between the plates has a magnitude of 1.04 103 V/m and is upward.
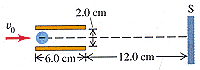
(a) What is the force (magnitude and direction) on the electron when it is between the plates?
(b) What is the acceleration of the electron (magnitude and direction) when acted on by the force in part (a)?
(c) How far below the axis has the electron moved when it reaches the end of the plates?
(d) At what angle with the axis is it moving as it leaves the plates?
(e) How far below the axis will it strike the fluorescent screen S?
F=Eq
F=ma
V=W/q
V=kq/r
I got parts a-c correct, a being 1.666e-16 N downward, b being 1.8473e14 m/s^2 downward, and c being .008118 meters.
Part d is giving me trouble. I've tried doing arctangent of .06/.008118, with .06 being the length of the plates and .008118 being how far down it travelled, but that didn't work. What am I doing wrong?
I'm also stuck on part e, but I think that's because I don't have part d.
Thank you!
Homework Statement
In Fig. 24-32 an electron is projected along the axis midway between the deflection plates of a cathode-ray tube with an initial speed of 6.40 106 m/s. The uniform electric field between the plates has a magnitude of 1.04 103 V/m and is upward.
(a) What is the force (magnitude and direction) on the electron when it is between the plates?
(b) What is the acceleration of the electron (magnitude and direction) when acted on by the force in part (a)?
(c) How far below the axis has the electron moved when it reaches the end of the plates?
(d) At what angle with the axis is it moving as it leaves the plates?
(e) How far below the axis will it strike the fluorescent screen S?
Homework Equations
F=Eq
F=ma
V=W/q
V=kq/r
The Attempt at a Solution
I got parts a-c correct, a being 1.666e-16 N downward, b being 1.8473e14 m/s^2 downward, and c being .008118 meters.
Part d is giving me trouble. I've tried doing arctangent of .06/.008118, with .06 being the length of the plates and .008118 being how far down it travelled, but that didn't work. What am I doing wrong?
I'm also stuck on part e, but I think that's because I don't have part d.
Thank you!
Last edited: