mrbec
- 4
- 0
- TL;DR
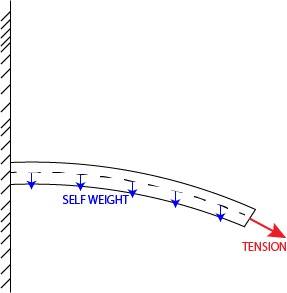
- Hello. I would like to know if applying tension to a cantilever beam at the free end affects the deflection it would have otherwise due to only its self weight, and if it does, how to calculate the deflection depending on the tension applied.
Not much to add since the question is fairly simple, but again I'm wondering if applying tension at the free end of a cantilever beam affects the deflection it would have if only itself weight is considered. Intuitively, tension should tend to straighten the beam, and if it does, how to calculate the resulting deflection? Please find below a simple illustration of the problem. Maybe I should also note that tension is always applied and not only after the beam is bent. Sorry for the simplicity of the question and thanks in advance.