Like Tony Stark
- 182
- 6
- Homework Statement
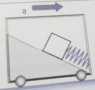
- The picture shows a block of ##0.5 kg## that interacts with a spring of constant ##40 \frac{N}{m}##. The body lies on a wedge and they are static with respect to the room that accelerates with ##a=0.5 \frac{m}{s^2}## to the right. The horizontal and the wedge form an angle of ##40°##. Determine the deformation of the spring, the normal force acting on ##A## and the acceleration needed to make the deformation equal to 0.
- Relevant Equations
- Newton's equations
I wrote Newton's equations for the block seen from the non inertial frame. The axis are inclined.
##x) Fe+W_x-f*cos(\alpha)=0##
##y) N-f*sin(\alpha)-W_y=0##
Where ##f*## is the pseudo-force and ##Fe## is the elastic force. I set the acceleration as 0 because they are in equilibrium.
The thing is that when I solve the equations I got that the deformation is negative, but it should be positive because the spring is being stretched.
##x) Fe+W_x-f*cos(\alpha)=0##
##y) N-f*sin(\alpha)-W_y=0##
Where ##f*## is the pseudo-force and ##Fe## is the elastic force. I set the acceleration as 0 because they are in equilibrium.
The thing is that when I solve the equations I got that the deformation is negative, but it should be positive because the spring is being stretched.