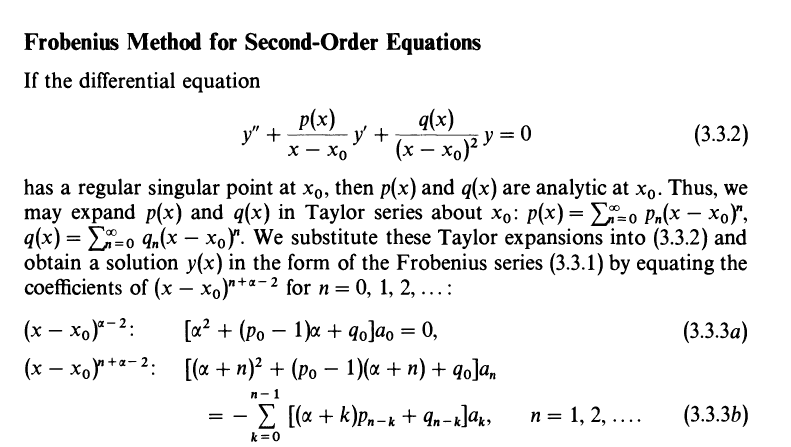Derivation for the indicial exponent in the Frobenius method

[Kloo]

I'm reading a book called Asymptotic Methods and Perturbation Theory, and I came across a derivation that I just couldn't follow. Maybe its simple and I am missing something. Equation 3.3.3b below. y(x) takes the form A(x)*(x-x0)^α and A(x) is expanded in a taylor series.

 

[pasmith]

Use $$\begin{split} \left(\sum_{n=0}^\infty a_nx^n \right)\left(\sum_{n=0}^\infty b_nx^n \right) &= \sum_{n=0}^\infty \sum_{m=0}^\infty a_n b_m x^{n+m} \\ &=\sum_{k=0}^\infty \left(\sum_{n=0}^n a_n b_{k-n}\right) x^k. \end{split}$$