Jhenrique
- 676
- 4
I'm studying classical mechanics and I'm stumbling in the quantity of differential identities.
Being S the action, H the hamiltonian, L the lagrangian, T the kinetic energy and V the potential energy, following the relationships:
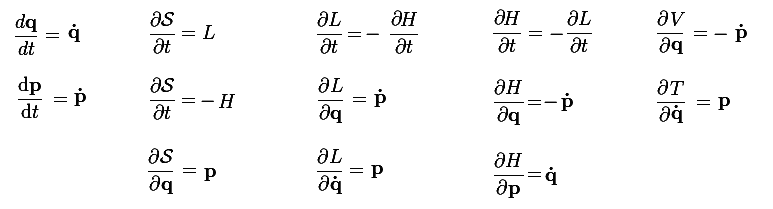
But, the big question is: that's all? Or has exist more?
Seems be missing
$$\frac{\partial S}{\partial q'} \;\;\; \frac{\partial S}{\partial p} \;\;\; \frac{\partial S}{\partial p'} \;\;\; \frac{\partial S}{\partial q'} \;\;\; \frac{\partial L}{\partial p} \;\;\; \frac{\partial L}{\partial p'} \;\;\; \frac{\partial H}{\partial p'} \;\;\; \frac{\partial H}{\partial q'} \;\;\; \frac{\partial V}{\partial q'} \;\;\; \frac{\partial V}{\partial p} \;\;\; \frac{\partial V}{\partial p'} \;\;\; \frac{\partial T}{\partial q} \;\;\; \frac{\partial T}{\partial p} \;\;\; \frac{\partial T}{\partial p'}$$
These relation exist? Make sense? If yes, how will be the identities?
Being S the action, H the hamiltonian, L the lagrangian, T the kinetic energy and V the potential energy, following the relationships:
But, the big question is: that's all? Or has exist more?
Seems be missing
$$\frac{\partial S}{\partial q'} \;\;\; \frac{\partial S}{\partial p} \;\;\; \frac{\partial S}{\partial p'} \;\;\; \frac{\partial S}{\partial q'} \;\;\; \frac{\partial L}{\partial p} \;\;\; \frac{\partial L}{\partial p'} \;\;\; \frac{\partial H}{\partial p'} \;\;\; \frac{\partial H}{\partial q'} \;\;\; \frac{\partial V}{\partial q'} \;\;\; \frac{\partial V}{\partial p} \;\;\; \frac{\partial V}{\partial p'} \;\;\; \frac{\partial T}{\partial q} \;\;\; \frac{\partial T}{\partial p} \;\;\; \frac{\partial T}{\partial p'}$$
These relation exist? Make sense? If yes, how will be the identities?