Derivation of the Boltzmann Distribution

[Peter Forbes]

I have a question about the Lagrange Multiplier method used to derive the Boltzmann distribution. I'm following the first http://en.wikipedia.org/wiki/Maxwell%E2%80%93Boltzmann_statistics" .

I can get to this equation fine:

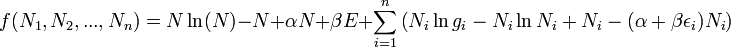
And I understand how they get the next line,
<br /> \frac{df}{dN_i}=\ln{g_i}-\ln{N_i}-(\alpha+\beta \epsilon_i)<br />
by considering N a constant when they do the partial differentiation.

However, since N=\sum_{i=1}^n N_i, can't I substitute that expression everywhere I have a N in the first equation? Then the differentiation gives me
<br /> \frac{df}{dN_i}=\ln{(\sum_{i=1}^n N_i)}+(\alpha-1)(\sum_{i=1}^n N_i)+\ln{g_i}-\ln{N_i}-(\alpha+\beta \epsilon_i)<br />

Which clearly has a different solution. Substituting for N before doing the partial derivative changes things...but why? I don't understand how one way should be any "more correct" than the other.

Thanks in advance.

 

[CompuChip]

Actually you misquoted the Wikipedia page, it doesn't say
<br /> \frac{df}{dN_i}=\ln{g_i}-\ln{N_i}-(\alpha+\beta \epsilon_i)<br />
but it says
<br /> \frac{\partial f}{\partial N_i}=\ln{g_i}-\ln{N_i}-(\alpha+\beta \epsilon_i).<br />

The difference is the d on the left-hand side. If you do a partial derivation (with the curly d) with respect to N_i then you get the result that is given, because we can treat N as a constant. If you do a complete derivation (with the straight d) then indeed you get some extra terms:
\frac{df}{dN_i} = \frac{\partial f}{\partial N_i} + \frac{\partial f}{\partial N} \frac{\partial N}{\partial N_i}
assuming that none of the other quantities (g_i, \epsilon_i, \ldots) depends on N_i implicitly.

In this case, the partial derivative is the correct one because you are allowing the N_i's to vary, but you have a constraint on N (namely that the total number of particles is fixed, so N cannot change - therefore it is no use varying N and seeing if the function can be made smaller).

 

[Peter Forbes]

OK, thanks for the help.
But I still don't understand why we can't replace N with N=\sum_{i=1}^n N_i in the equation before we do the partial differentiation.

Note the first equation could be written
f(N_1,...N_n)=N\ln(N)-N + \alpha N + \beta E + N \sum_{i=1}^n (N_i \ln(g_i) - N_i \ln (N_i)-(\alpha+\beta \epsilon_i) N_i)

Where I've put the N outside the sum rather than the Ni's inside the sum. But the Ni's inside the sum are not treated as constants.

I understand that the partial derivatives mean keeping everything but the one variable constant. But there are equivalent ways of writing the same expression, which gives different answers after partial differentiation.

So I guess my question is, how would one know what form is the "correct one" to use before applying the partial differentiation?