grace77
- 43
- 0
Problem statement

My question is for number 27.
Revelant equation
None
Attempt at a solution
I'm not sure where to start.
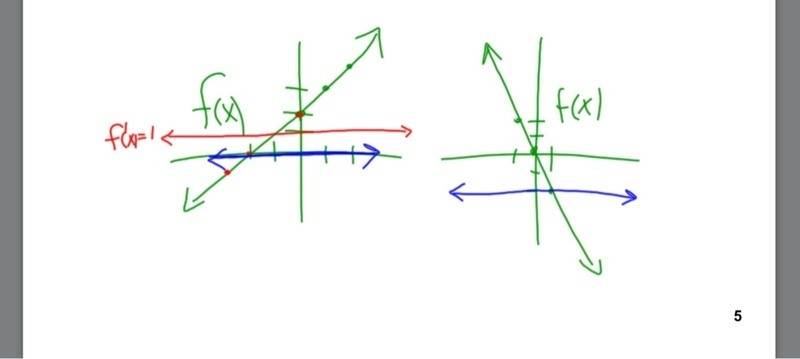

This is my teachers answer. I understand how the slope is 1 for x greater than -1 and that it is -2 at x greater than -1 and that there is a point at (0,-1) but I don't understand how they connect to form that final pic. I think I'm missing something ,can someone help me?
My question is for number 27.
Revelant equation
None
Attempt at a solution
I'm not sure where to start.
This is my teachers answer. I understand how the slope is 1 for x greater than -1 and that it is -2 at x greater than -1 and that there is a point at (0,-1) but I don't understand how they connect to form that final pic. I think I'm missing something ,can someone help me?