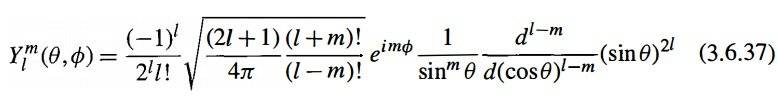I Deriving Spherical Harmonics from Sakurai's Book

[davidge]

Hi everyone. I'm looking for a derivation of the Spherical Harmonics that result in the form below given in Sakurai's book. I looked up on web and I found just that these are related with Legendre Polynomials. Has anyone a source, pdf, or similar to indicate me? (I would appreciate a derivation that uses the same notation as Sakurai.)

 

[Charles Link]

I think you could try looking at J.D. Jackson's "Classical Electrodynamics". I loaned out my copy of the book a while back, but I think it is likely to be in there.

 

[blue_leaf77]

That should be derivable from the Rodrigues formula for Legendre polynomials. The keywords that might be of interest for you are "Rodrigues formula" and "associated Legendre polynomial".

 

[vanhees71]

The key is to start with the abstract formalism, i.e., to build the irreducible representations of the angular-momentum algebra,
$$[\hat{J}_a,\hat{J}_b]=\mathrm{i} \epsilon_{abc} J_c,$$
where I've set $\hbar=1$ for convenience.

It turns out that you can build common eigenvectors of $\vec{\hat{J}}^2$ and $\hat{J}_z$, using the "ladder operators" $\hat{J}_{\pm}=\hat{J}_1 \pm \mathrm{i} \hat{J}_2$. Then you can show that for the special case of orbital angular momentum, were the components are given by
$$\hat{\vec{L}}=\hat{\vec{x}} \times \hat{\vec{p}},$$
only the integer irreps, i.e., for $l= \in \{0,1,2,\ldots\}$ occur.

To map this formalism you realize the Hilbert space as $\mathrm{L}^2(S)$, where $S$ is the unit sphere. As coordinates you can take $(\vartheta,\varphi)$, i.e., the angles of the usual spherical coordinates parametrizing the sphere in $\mathbb{R}^3$. Then you can construct the spherical harmonics with help of the ladder operators, leading easily to the above given Rodriguez formula, the scalar products/norms of the eigenstates etc.

 

[DrClaude]

Have look at http://mathworld.wolfram.com/SphericalHarmonic.html and links therein.

 

[davidge]

@vanhees71 It sounds interesting to use this method to derive them. I already know something about what you mentioned on angular momentum (from Sakurai's book). Can you show me just the beginning of the derivation using these angular momentum relations, Ladder operators, etc?

@DrClaude, @blue_leaf77, @Charles Link Now I'm thinking it would be better to me to find a way to relate Legendre Polynomials and Rodrigues formula to the Sph. Harmonics, something like a guide to put the equations in a form such that I can use Legendre Polynomials and Rodr. formula to solve them.

 

[blue_leaf77]

Legendre polynomial of order $l$, namely $P_l(x)$, can alternatively be computed using Rodrigues formula
$$
P_l(x) = \frac{1}{2^l l!} \frac{d^l}{dx^l} (x^2-1)^l
$$
Then there is this associated Legendre polynomial whose relation to the Legendre polynomial is given by
$$
P_{lm}(x) = (-1)^m (1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x)
$$
Finally the spherical harmonics is just proportional to the associated Legendre polynomial, which exact equation I leave to you to find in the internet. By making change of variable $x=\cos \theta$ you should get the above Rodrigues formula for spherical harmonics.
The procedure I offer above is the use-this-use-that type. If you want a more formal prove, you should follow vanhees's suggestion.

 

[vanhees71]

@vanhees71 It sounds interesting to use this method to derive them. I already know something about what you mentioned on angular momentum (from Sakurai's book). Can you show me just the beginning of the derivation using these angular momentum relations, Ladder operators, etc?

I have this in my QM manuscript, which however is in German. Perhaps, you can follow it since the "formula density" is quite high (Section 4.1, p101ff):

http://theory.gsi.de/~vanhees/faq-pdf/quant.pdf

In the html version of this text it's here:

http://theory.gsi.de/~vanhees/faq/quant/node53.html

 

[davidge]

@vanhees71 Awesome manuscript, thank you so much. This was very helpful. I'm using google to translate some parts of the text.

 

[Khashishi]

It's wonderful that math is a near universal language.

 

[davidge]

It's wonderful that math is a near universal language

I agree with you. In fact, seeing the equations is enough to me. I'm translating only a few words actually.

 

[davidge]

@vanhees71 I would like to ask you just how do we go from $U_{l\ l} (u)$ in (4.1.72) to $U_{l\ m} (u)$ in (4.1.73), p. 109 of your paper. I noticed that the coefficient $c_{l\ l}$ has its terms changed and also I'm not getting why that derivative appears in (4.1.73).

I guess it can be made by continuously changing (4.1.71), starting on it with $m = l$ and obtaining on the left-hand-side a $U(u)$ with one lower value of $m$ each time. Is this correct? If so, how do we know when it's time to stop lowering values of $m$?

 

[vanhees71]

Directly after (4.1.73) I also give a proof by induction.

If you look at (4.1.73), you see that the polynomial $(1-u^2)^l=(-u)^{2l}+\cdots$, i.e., the highest power in the polynomial is $2l$. So if you take derivatives of order $k>2l$ you get 0, as it should be.