Mr_Acceleration
- 3
- 0
With the assumptions of Inviscid flow, no pressure gradient and no body force terms in 1-D Navier Stokes becomes 1-D nonlinear convection equation;
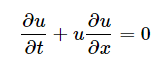
And if we assume velocity of wave propagation is constant value c, equation becomes 1-D linear convection equation;
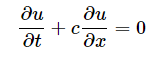
This is online derivation and my question is why only the u value outside of partial derivatives is replaced with c? we have 3 u term there. I was thinking they were all same term. So why do we only replace one of them?
And if we assume velocity of wave propagation is constant value c, equation becomes 1-D linear convection equation;
This is online derivation and my question is why only the u value outside of partial derivatives is replaced with c? we have 3 u term there. I was thinking they were all same term. So why do we only replace one of them?