Designing a spiral with a certain angle relative to movement direction

[DefinitelyAnEnjinear]

TL;DR

Designing a spiral with a 45 degree angle relative to the movement of a disk orbiting around a point

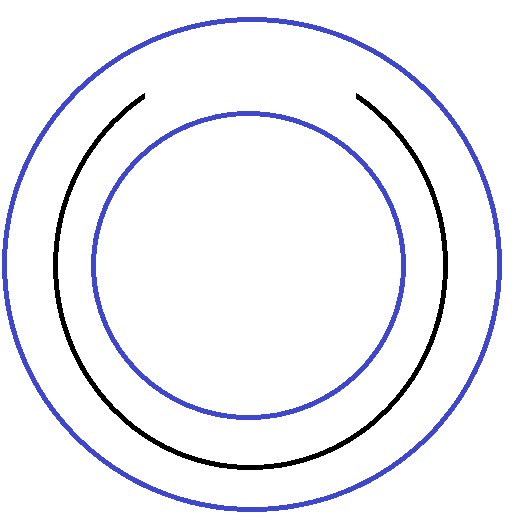
I have a disk traveling on the inner blue track (let's say the blue part is the center of the disk).
I want to push the disk outside (as the disk is traveling in a circle) to the outer track.
The black part is the wall separating the tracks

To that end, I've made some calculations, but I have some concerns regarding my results, and am wondering if there's a better way to go about it.
I have a decent math background, but no engineering background at all.

I started out by noting the direction of movement for the disk, say it's moving counter-clockwise. If c is a point on the inner circle (for simplicity: unit circle), then the movement direction is determined as follows:

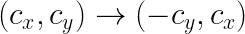
Also, some relevant trigonometric identities:

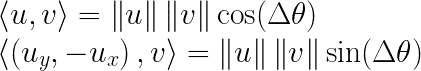
where Δθ is the angle between u and v.

Let's say I want a 45 degree angle between my spiral and the movement direction of the disk (my very limited physics knowledge tells me a steeper angle would require more force to be applied because more of the "equal and opposite reaction" thing would be in the direction that's against the disk movement. Obviously a smaller angle would mean it takes longer to get the disk as far as I need it to go).
The sine and cosine of 45 degrees go without saying, yielding:

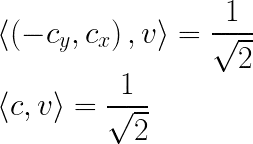
And after doing some math^TM

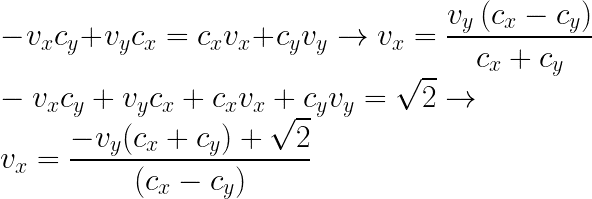
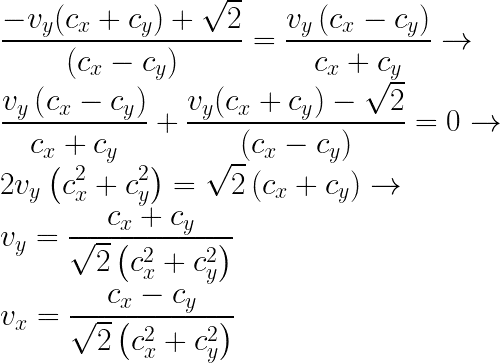
So now we have v, which... I'm not sure how to put this into words in a technically accurate way, so let's say it's the direction of the tangent to the spiral. Meaning its slope is that of the derivative. Meaning:

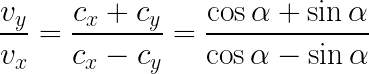
is the derivative of the function describing my spiral, with α being the angle between the x-axis and the vector pointing to some point on the circle.

This is the part where I start to get worried and confused, because (1) I potentially have a division by 0 here, and (2) the point is to move the disk during rotation and I'm not sure if my reasoning still holds at this point.

With a little help from wikipedia I got to:

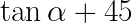
Being my derivative.
So if, say, I wanted to start the transition when we're at 45 degrees... I start off on a singularity.

So, did I get anything wrong? Is there a better approach to solving this problem?

 

[hutchphd]

Try researching "equiangular spiral" (or Bernoulli spiral or logarithmic spiral). Does that help?

 

[Lnewqban]

What is driving the rotation and what is forcing the disc to follow the circular trajectories and switch from one to another?

 

[DefinitelyAnEnjinear]

Try researching "equiangular spiral" (or Bernoulli spiral or logarithmic spiral). Does that help?

A brief look tells me the distances increase geometrically as opposed to an Archimedean spiral where the distances increase by a constant. Is this really what I should be looking at? my intuition tells me I need distances that increase by a constant, don't I?

Edit: I see now that the angle remains a constant according to wikipedia. counter-intuitive to me but it definitely seems like the answer.

What is driving the rotation and what is forcing the disc to follow the circular trajectories and switch from one to another?

The disk will have a pin in it that will be able to move back and forth in a slot in a gear which will be driven.
There will be a wall preventing the disk from switching tracks until it reaches the point
I didn't want to complicate the question with details that seem unimportant.

 

[hutchphd]

intuitive to me but it definitely seems like the answer.

What I find interesting (and obvious, after you see it!) is that the spiral is self-similar: If you "blow it up" uniformly it can be laid atop the smaller version exactly (with a rotation). Of course that follows from the equal angle requirement. Fun.

 

[Lnewqban]

...
The disk will have a pin in it that will be able to move back and forth in a slot in a gear which will be driven.
There will be a wall preventing the disk from switching tracks until it reaches the point
I didn't want to complicate the question with details that seem unimportant.

I see.
Thank you.