Designing an Op-Amp with Variable Gain: Need Advice

[Number2Pencil]

Homework Statement

Design an op-amp that uses a variable 50k ohm resistor. when this variable resistor is at one extreme, the gain is 13, and at the other extreme, the gain is 3. you may use up to 2 op-amps, and up to 7 resistors (including the variable resistor)

The Attempt at a Solution

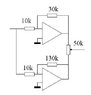
here is the circuit i came up with:

I made it so all I would have to find is Rf to satisfy the design.

here is how I solved for Rf

first extreme:

(1 + \frac{R_f}{60k-ohms}) = 13

next extreme:

(1 + \frac{R_f}{110k-ohms}) = 3

combine the two equations:

11 + \frac{R_f}{110k-ohms} = 1 + \frac{R_f}{60k-ohms}

10 = R_f (\frac{1}{60k-ohms} - \frac{1}{110k-ohms})

R_f = 1.32M-ohms

this answer gives a gain of 13 on one extreme of the variable resistor and 23 on the other. whoops. any help?

 

[Gokul43201]

Two equations in one variable? Why should they have the same solution? As expected, if you solve them individually, you find they do not.

How would you fix this?

 

[Number2Pencil]

you're right, I get a different resistor values for each equation, yet it needs to be the same value.

Mathematically, I should have one equation for each variable. There's only one but I forget how to solve an equation that has an answer of 3 OR 13...

either i need more variables or i need less equations

yeah i need another pointer

 

[Number2Pencil]

What I make the 60kohm resistor R1 (or another unknown)...

that way I could have two equations with two unknowns. Is this the correct way to approach this problem?

 

[Gokul43201]

Yes, that would be one way to fix it. To solve a problem with n independent boundary values, you need n independent parameters.

 

[Number2Pencil]

Good, cause it worked. I got R1 = 10k ohm and Rf = 120k ohm which give me the correct gain(s). Thank you so much I appreciate all the help this forum gives me.

But out of curiousity, you said that's "one" way to solve it. got another trick up your sleeve?

 

[AlephZero]

But out of curiousity, you said that's "one" way to solve it. got another trick up your sleeve?

There are a huge number of ways you could design the circuit within the constraints you are given. For example this is a completely different idea which doesn't need any algebra to figure it out.

(Except its deliberately wrong because it has gains of -3 to -13, so its not a complete solution to your question!)

 

[berkeman]

(Except its deliberately wrong because it has gains of -3 to -13, so its not a complete solution to your question!)

Getting kind of sneaky there, are we?

 

[Gokul43201]

But out of curiousity, you said that's "one" way to solve it. got another trick up your sleeve?

I would have put the trimpot on the feedback loop, instead of as an input resistor.

 

[Number2Pencil]

yeah, i realized it today that by putting the trimmer on the feedback, i'd get the low, 3 gain when it's shorted and 13 when it's the full 50k, which would just make it less confusing to use