Destructive Interference in Thin Film Interference

[willydavidjr]

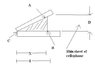
Two oblong pieces of plane glass are separated from each other by a thin sheet of cellophane and held together with rubber bands, as shown in figure(I provided a website for the figure below), where the amount of separation is much exaggerated. If you place a "sodium vapor lam" vertically above the glass plates, you will observe an alternate series of very close bright and dark lines. A light wave is reflected at point A and simply forms a returning wave. Some of the original light wave crosses the narrow air gap and is reflected at point B. If it advances across the air gap as a trough, then it is reflected at point B as a crest.

Question: The length of the wedge-shaped space between the two glasses is l, the thickness of the thin sheet of cellophane is d, and the distance between point C and point A (or B) is x as shown in the figure.Supposing the result is destructive interference or darkness. Find the relation between x, \lambda,l and d.

My idea:
I think their relation is x=\frac{l}{2d} \lambda(n + \frac{1}{2})


This is the website: www.geocities.com/willydavidjr/interference.html

 

[mukundpa]

At A the ray is reflected from rarer medium (air) and at B it is reflected from denser medium (glass). When a wave is reflected from a denser medium an additional path difference of (lembda/2) is to be considered. Did you considered this additional path difference?