Determine the tension in the cable attached to the chair

[abstrkt]

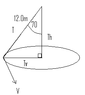
A "swing" ride at a carnival consists of chairs that are swung in a circle by 12.0 m cables attached to a vertical rotating pole, as the drawing shows. ( = 70.0°) Suppose the total mass of a chair and its occupant is 200 kg

(a) Determine the tension in the cable attached to the chair.

(b) Find the speed of the chair.



I'm really lost..can anyone help me?

 

[cobhc]

i couldn't really help with this question without working through it. So,
try reading it a stage at a time and understanding it fully before moving on.
This will hopefully help you to understand it further

firstly, see attached diagram to go with this question.
First we must resolve the tension in the vertical direction (Tv)
in centripetal questions like this Tv = Mg (or the weight)
so
Tv = 200 x 9.81
Tv = 1962N

Since we know the angle we can now find T using trigonometry
so
T (or the hypotenuse H) = 1962/cos 70
T = 5737N


Now to find the velocity (v)
firstly we must find the tension in the radius or horizontal (Th). We do this the same way as we found the overall tension in the rope, using trig, so:

Th = 1962 tan 70
Th = 5391N but we know Th = (M.v^2)/r
so substituting between formulas we get
5391 (Th) = (200(M) x V^2)/12 sin 70 where 12 sin 70 is the radius(in metres)

re-arranging to find
(5391 x 11.3)/200 = V^2
V = 17.5 m/s^-1

hope this helps and is right, I've kinda rushed a bit though so check it

cobhc

btw, what school year was this set for?

 

[quicknote]

I would approach this problem by using the principles of Newton's laws of motion and basic kinematics.

(a) To determine the tension in the cable attached to the chair, we can use Newton's second law which states that the net force acting on an object is equal to its mass multiplied by its acceleration (F=ma). In this case, the chair and its occupant have a combined mass of 200 kg. The only forces acting on the chair are the tension in the cable and the weight of the chair and occupant, which can be represented by the force of gravity (mg).

Since the chair is moving in a circular motion, it is accelerating towards the center of the circle. This acceleration can be calculated using the equation a=v^2/r, where v is the velocity of the chair and r is the radius of the circle (which is equal to the length of the cable, 12.0 m).

Therefore, the net force acting on the chair is equal to the tension in the cable minus the force of gravity: Fnet = T - mg. We can rearrange this equation to solve for the tension in the cable: T = Fnet + mg.

Substituting the values, we get: T = (200 kg)(v^2/12.0 m) + (200 kg)(9.8 m/s^2).

Since we are given the angle of the cable (70.0°), we can use trigonometry to find the vertical component of the force of tension, which is equal to Tsinθ.

Therefore, the tension in the cable attached to the chair is T = (200 kg)(v^2/12.0 m) + (200 kg)(9.8 m/s^2)sin70.0°, which gives us a value in Newtons (N).

(b) To find the speed of the chair, we can use the equation v = ωr, where ω is the angular velocity (which is equal to the speed of rotation) and r is the radius of the circle.

We can calculate ω using the equation ω = 2π/T, where T is the time it takes for the chair to complete one full rotation. Since we don't have this information, we can use the equation T = 2πr/v, where r is the radius of the circle (12.0 m) and