Determine the total force on a dam

[Firben]

Homework Statement

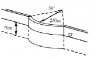
Determine the total force the water exerts on a cylindrical bent dam, with radius 250m and the opening angle of 50 degrees. The deep of the water is 70m

Homework Equations

The Attempt at a Solution

F = p_cA (1)
F_x = ρgζ_cxA_x (2)
ζ_p´ = ζ_c´ + I_c/(ζ_c´ * A) (3)
ζ_p' = ζ (4)
ζ_cx = h_c (5)

I got I_c = r*sinα/α (6) from physics handbook

I'm not sure if A = h∏r^2 is correct or if h_c = a/2 is correct (a is the height)Is this right ? or is something missing ?

 

[Arkavo]

Ans will be approximately 51.77E8 N

 

[CWatters]

Perhaps I made a mistake but I got about 61 x 10^8 N.

 

[mfb]

F = p_cA (1)
F_x = ρgζ_cxA_x (2)
ζ_p´ = ζ_c´ + I_c/(ζ_c´ * A) (3)
ζ_p' = ζ (4)
ζ_cx = h_c (5)

Can you explain all those parameters you introduced?

Do you have some definition of "total force"? Net force for the whole dam, added as vector? Or force per area, integrated over the area independent of the direction?
Do we subtract the atmospheric pressure?
With g=10m/s^2 and with subtracted atmospheric pressure I get the same result as Arkavo in one of those cases. With g=10m/s^2, without subtracted atmospheric pressure and with the other method (!), I get CWatters' result.

 

[CWatters]

Just for info.. I worked out the area. Then I worked out the average pressure (eg I halved the pressure at 70m) and multiplied the two.

 

[haruspex]

Just for info.. I worked out the area. Then I worked out the average pressure (eg I halved the pressure at 70m) and multiplied the two.

I don't think that's valid. I would take total force to mean net force, so all the little forces on elemental areas need to be added vectorially, implying some cancellation.

Edit: On that basis, I get 5.08E9.

 

[Firben]

I'm not sure about the area, its the net force on the dam

 

[CWatters]

I don't think that's valid. I would take total force to mean net force, so all the little forces on elemental areas need to be added vectorially, implying some cancellation.

Edit: On that basis, I get 5.08E9.

Ah yes I see what you are getting at.

Do you get the same answer if you work out the length of the chord. Multiply that by 70 and the average pressure?

 

[mfb]

As far as I can see, we now have 8 possible numerical results.

a) vector integration of force ("net force")
A) integration of magnitude of force

b) subtracting atmospheric pressure
B) not subtracting atmospheric pressure

c) g=10m/s^2
C) g=9.81m/s^2

For each category, one option can be picked.
Arkavo calculated Abc, CWatters calculated aBc, haruspex calculated AbC.

 

[haruspex]

Do you get the same answer if you work out the length of the chord. Multiply that by 70 and the average pressure?

That's what I did.

 

[Firben]

It is the total force on the dam. The answer is F = 5.1*10^9 N. What is the area ? 2pi*r? The pressure is that the water pressure at 20 degres? And the length of the chord is that 2*250tan50?

I got it be 2.57*10^9 N

F = 1000*9.81*70*2pi*250tan50

 

[mfb]

2 pi r is the circumference of a circle. There is no circumference involved here. To get 5.1, follow Arkavo: Calculate the pressure at a depth of 35m (starting with 0 at zero depth), multiply it with 70m and the length of the dam.
I think you can just multiply your result with 2 to get the same thing.

 

[haruspex]

the length of the chord is that 2*250tan50?

No, it's 2*250*sin(50^o/2)

 

[Arkavo]

why not just take flux of force on a small strip of area and integrate from 0-70m