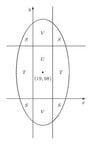
Determine the value of A1 - A2 + A3 - A4

[anemone]

Let $$A_1$$, $$A_2$$, $$A_3$$ and $$A_4$$ represent the areas within the ellipse $$\frac{(x-19)^2}{19}+\frac{(y-98)^2}{98}=1998$$ that are in the first, second, third and fourth quadrants respectively. Determine the value of $$A_1-A_2+A_3-A_4$$

 

[anemone]

Re: Determine the value of A1-A2+A3-A4

I must mention here that the idea of this problem came from Professor Gregory Galperin of Eastern Illinois State University, U.S.A. and I feel so grateful and thankful to Professor Gregory Galperin for approving me to show his solution to this problem at this site.

Solution:

We know that the center of the ellipse is the point (19, 98). The two vertical lines $$ x=0 $$ and $$x=2\cdot19=38$$ and the two horizontal lines $$y=0$$ and $$y=2\cdot98=196$$ divide the ellipse into nine regions, as shown below.

View attachment 801

Then, in terms of the areas marked by S, T, U and V, we find that $$A_1=U+V+S+T$$, $$A_2=S+T$$, $$A_3=S$$, and $$A_4=V+S$$, and therefore

$$A_1-A_2+A_3-A_4=(U+V+T+S)-(S+T)+S-(V+S)=U.$$

Hence the answer is $$38\cdot196=7448$$.Note:
This solution was published in the book by G. Berzsenyi "International Mathematics Talent Search, Part 2 ", AMT Publishing(2011). The problem was given at the Round 29, and it's titled as Problem 5/29; the pages are: the formulation @ p.11, and the solution @ p.84.