Determing the center of gravity of a shaded section

[Guillem_dlc]

Homework Statement

Determine the volume of the shaded area around the Y-axis by using the theorem of Pappus Guldinus, where value of R = 143,3 cm.

a) Determine the area of the shaded section.

b) Determine the center of gravity of the shaded section.

c) Detrmine the volume by using the theorem of Pappus Guldinus.

Relevant Equations

theorem of Pappus Guldinus, center of gravity

Determine the volume of the shaded area around the Y-axis by using the theorem of Pappus Guldinus, where value of R = 143,3 cm.
a) Determine the area of the shaded section.
b) Determine the center of gravity of the shaded section.
c) Detrmine the volume by using the theorem of Pappus Guldinus.

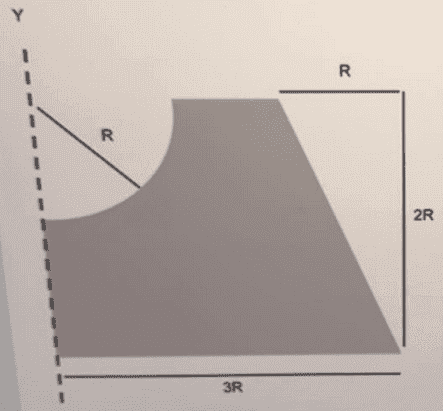
My attempt at the solution:

a) $A_T=2R\cdot 2R-\dfrac14 \cdot \pi \cdot R^2+\dfrac{R\cdot 2R}{2}$
$A_T=4R^2-\dfrac{\pi \cdot R^2}{4}+R^2=4\cdot 143,3^2-\dfrac{\pi \cdot 143,3^2}{2}+143,3^2=86546,39\, \textrm{cm}^2=\boxed{8,65\, \textrm{m}^2}$

b) I consider three figures to calculate the centres of gravity:
Figure 1 (Rectangular triangle with side R and hypotenuse 2R) --> $\bar{x}=2R+\dfrac{R}{3}=2\cdot 143,3+\dfrac{143,3}{3}=334,36\, \textrm{cm}$
$\bar{y}=\dfrac{2R}{3}=\dfrac{2\cdot 143,3}{3}=95,53\, \textrm{cm}$
Figure 2 (Square of side 2R) --> $\bar{x}=\dfrac{2R}{2}=R=143,3\, \textrm{cm}$
$\bar{y}=\dfrac{2R}{2}=R=143,3\, \textrm{cm}$
Figure 3 (sector of circle)--> $\bar{x}=\dfrac{4r}{3\pi}=\dfrac{4\cdot 143,3}{3\pi}=60,82\, \textrm{cm}$
$\bar{y}=2R-\dfrac{4R}{3\pi}=2\cdot 143,3-\dfrac{4\cdot 143,3}{3\pi}=225,78\, \textrm{cm}$
Then:
$\bar{x}=\dfrac1A\sum_{i=1}^n \bar{x_i}A_i=\dfrac{334,36\cdot 143,3^2+143,3\cdot 4\cdot 143,3^2-60,82\cdot \frac{\pi \cdot 143,3^2}{2}}{86546,39}=192,67$

This last result would be correct?

Thanks

 

[haruspex]

The image seems to show the Y axis as at some angle to the side of length 2R. But there does not seem to be enough information to determine that angle.
Are they parallel really, and the image is taken at some angle to the page?

 

[etotheipi]

The image seems to show the Y axis as at some angle to the side of length 2R. But there does not seem to be enough information to determine that angle.
Are they parallel really, and the image is taken at some angle to the page?

I think it's constructed from a rectangle of dimensions 3R x 2R attached to the y-axis like a flag, then with a right triangle removed from the right and a quarter circle removed from the top left.

 

[haruspex]

I think it's constructed from a rectangle of dimensions 3R x 2R attached to the y-axis like a flag, then with a right triangle removed from the right and a quarter circle removed from the top left.

Yes, if the 2R and Y axis are indeed parallel.
@Guillem_dlc , you make life hard for yourself and anyone reading your work by plugging in numbers much too soon. Write it out again all in terms of R. Don't plug in its value until the very end.
There are lots of advantages to this style, one of which is that more readers will try to help you.

 

[etotheipi]

Yes, if the 2R and Y axis are indeed parallel.

Ah, I see what you mean. I guess since no further information is given we just have to assume it's sloppiness on the question setter's part!

As an aside, I must admit I'd never heard of 'Pappus-Guldinus' but the result looks almost too simple to be true! I haven't read through the proof yet but at the moment it seems a bit like magic. Add that to the fact that when I said the name out loud my furniture started floating...

 

[haruspex]

assume it's sloppiness on the question setter's part!

No, I wouid guess it is reasonably obvious in the original diagram, but the distortion in the way the photo has been taken makes it hard to believe.

 

[Guillem_dlc]

The image seems to show the Y axis as at some angle to the side of length 2R. But there does not seem to be enough information to determine that angle.
Are they parallel really, and the image is taken at some angle to the page?

Yes, Y and 2R are parallel.

 

[Guillem_dlc]

Yes, if the 2R and Y axis are indeed parallel.
@Guillem_dlc , you make life hard for yourself and anyone reading your work by plugging in numbers much too soon. Write it out again all in terms of R. Don't plug in its value until the very end.
There are lots of advantages to this style, one of which is that more readers will try to help you.

Okay, I'll do it by leaving R indicated and I'll pass it around. You're absolutely right.

 

[Guillem_dlc]

Ah, I see what you mean. I guess since no further information is given we just have to assume it's sloppiness on the question setter's part!

As an aside, I must admit I'd never heard of 'Pappus-Guldinus' but the result looks almost too simple to be true! I haven't read through the proof yet but at the moment it seems a bit like magic. Add that to the fact that when I said the name out loud my furniture started floating...

Yes

 

[TSny]

As an aside, I must admit I'd never heard of 'Pappus-Guldinus' but the result looks almost too simple to be true! I haven't read through the proof yet but at the moment it seems a bit like magic. Add that to the fact that when I said the name out loud my furniture started floating...

 

[Guillem_dlc]

Writing in terms of $R$:

a) $A_T=2R\cdot 2R-\dfrac14 \pi R^2+\dfrac{R2R}{2}=4R^2-\dfrac{\pi R^2}{4}+R^2=\dfrac{16R^2-\pi R^2+4R^2}{4}=\dfrac{R^2\cdot (20-\pi)}{4}=\dfrac{20R^2-\pi R^2}{4}=143,3\, \textrm{cm}=1,433\, \textrm{m}$

b) Centers of gravity:
- Figure 1: $\bar{x}=2R+\dfrac{R}{3}=\dfrac{6R+R}{3}=\dfrac{7R}{3}$
- Figure 2: $\bar{x}=\dfrac{2R}{2}=R$
- Figure 3: $\bar{x}=\dfrac{4R}{3\pi}$
Then:
$\bar{x}=\dfrac1A \sum_{i=1}^n \bar{x_i}\cdot A_i=\dfrac{\frac{7R}{3}+R+\frac{4R}{3\pi}}{\frac{20R^2-\pi R^2}{4}}=\dfrac{\frac{7R+3R}{3}+\frac{4R}{3\pi}}{\frac{20R^2-\pi R^2}{4}}=\dfrac{\pi (7R+3R)+4R}{3\pi}: \dfrac{20R^2-\pi R^2}{4}=\dfrac{4\pi \cdot (7R+3R)+16R}{3\pi \cdot (20R^2-\pi R^2)}=\dfrac{R\cdot (4\pi \cdot (7+3)+16)}{3\pi R^2(20-\pi)}=\dfrac{40\pi +16}{3\pi R(20-\pi)}=\dfrac{40\pi +16}{3\pi \cdot 143,3(20-\pi)}=0,622\, \textrm{m}$

So I know the result is not right but I can't find the mistake.

 

[haruspex]

$\bar{x}=\dfrac1A \sum_{i=1}^n \bar{x_i}\cdot A_i=\dfrac{\frac{7R}{3}+R+\frac{4R}{3\pi}}{\frac{20R^2-\pi R^2}{4}}$

What you have written in the numerator is $\sum_{i=1}^n \bar{x_i}$, not $\sum_{i=1}^n \bar{x_i}\cdot A_i$.

 

[Guillem_dlc]

What you have written in the numerator is $\sum_{i=1}^n \bar{x_i}$, not $\sum_{i=1}^n \bar{x_i}\cdot A_i$.

$\bar{x}=\dfrac{\frac{7R}{3}\cdot R^2+R\cdot 4R^2-\frac{4R}{3\pi}\cdot \frac{\pi R^2}{4}}{\frac{20R^2-\pi R^2}{4}}=\dfrac{\frac{7R^3}{3}+4R^3-\frac{4\pi R^3}{12\pi}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{\frac{7R^3}{3}+4R^3-\frac{R^3}{3}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{\frac{7R^3+12R^3-R^3}{3}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{18R^3}{3}:\dfrac{R^2\cdot (20-\pi)}{4}=\dfrac{72R^3}{3R^2\cdot (20-\pi)}=\dfrac{24R}{20-\pi}$
Then,
$\bar{x}=\dfrac{24\cdot 143,3}{20-\pi}=204,005\rightarrow \boxed{2,04\, \textrm{m}}$

Now, is it correct?

 

[haruspex]

$\bar{x}=\dfrac{\frac{7R}{3}\cdot R^2+R\cdot 4R^2-\frac{4R}{3\pi}\cdot \frac{\pi R^2}{4}}{\frac{20R^2-\pi R^2}{4}}=\dfrac{\frac{7R^3}{3}+4R^3-\frac{4\pi R^3}{12\pi}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{\frac{7R^3}{3}+4R^3-\frac{R^3}{3}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{\frac{7R^3+12R^3-R^3}{3}}{\frac{R^2\cdot (20-\pi)}{4}}=\dfrac{18R^3}{3}:\dfrac{R^2\cdot (20-\pi)}{4}=\dfrac{72R^3}{3R^2\cdot (20-\pi)}=\dfrac{24R}{20-\pi}$
Then,
$\bar{x}=\dfrac{24\cdot 143,3}{20-\pi}=204,005\rightarrow \boxed{2,04\, \textrm{m}}$

Now, is it correct?

Looks right.

 

[sysprog]

Please think of Pappus' simple and brilliant idea as a clue to doing the triple integral that you have to do when you are modeling Homer Simpson eating a donut. When does the centroid exit the empty space at the donut hole and actually enter the material of the remaining portion of the donut (torus/toroid)? The theorem is like if an anaconda swallowed a DVD and had to pass it at maximum area all the way down its alimentary canal.