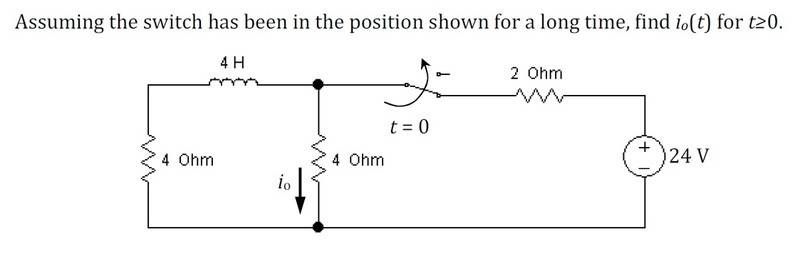
R0CC0 said:
So that would give me an answer of io(t) = 4.8e-2t ??
You've got the right form of the equation but still the wrong initial current.
We're assuming the circuit is at steady state just before the switch is thrown. This means all the currents and voltages in the circuit are constant.
Take a look at the equation governing the V/I relationship of an inductor: V=L di/dt. If all currents are constant, what does that say about the voltage across the inductor? Does that make it easier to find the steady current flowing through the inductor?===== a little extra
I just want to add (and then correct a mistake I made above!), when you know the response is first order, you always know the voltage or current will follow either Ae
-t/τ or A(1-e
-t/τ). You just need to know what the voltage/current is at t=0 and what it is at t->∞ to know which of these the result is. That, added to knowledge of what τ is -- L/R in RL circuits and RC in RC circuits, is a very useful shorthand to get circuit behaviour for first order circuits. (The R in the time constant equations is the R seen by the inductor or capacitor).
If you don't have a trick at hand for higher order circuits, you have to solve the usual way. Incorporating initial conditions for inductors and capacitors comes directly from the Laplace transform. Inductors: v=L di/dt -> V(s) = sL I(s) - Li(0), Capacitors: i = C dv/dt -> I(s) = sC V(s) - Cv(0). Notice how in the laplace domain, an inductor looks like a resistor of value sL in series with a battery of value -Li(0) (The voltage V(s) appears across the two in series). Also a capacitor looks like an admittance of sC-- equivalently an impedance of 1/sC -- with a current source of -Cv(0) in parallel.
I don't know if you've studied that yet, but above I said you could replace the inductor with an inductor in parallel with a current source to model its initial condition. Actually
I should have said the inductor could be modeled as an unenergized inductor in series with a battery of -Li(0) volts
(the sign acts to generate the initial current direction). If you put that into the circuit, you could solve the usual way for circuit behaviour including initial conditions.