Diff Eq-Particular solution with fourier cosine/sine series

[frozenguy]

Diff Eq--Particular solution with Fourier cosine/sine series

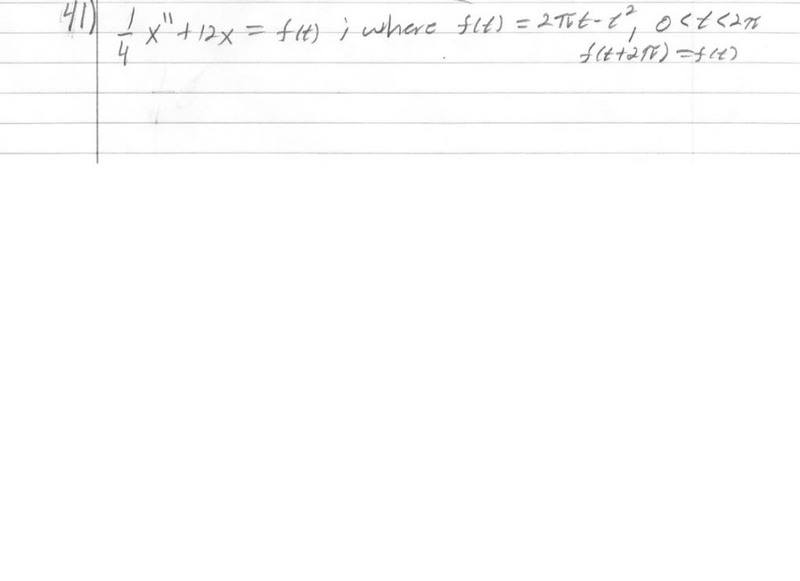
Homework Statement

Find the particular solution x_p(t) of equation $$m\frac{d^{2}x}{dt^{2}}+kx=f(t)$$ when $$m=\frac{1}{4}$$ , k=12, f(t) is given. Assume that when f(t) is extended to the negative t-axis in a periodic manner, the resulting function is even.

The Attempt at a Solution

So, What does it mean to extend f(t) to the negative t-axis in a periodic manner? And what does it mean when an example in the book says a 2p-periodic extension?
And how do I use $$f(t+2\pi)=f(t)$$
Thanks for looking!

 

[jackmell]

So, What does it mean to extend f(t) to the negative t-axis in a periodic manner? And what does it mean when an example in the book says a 2p-periodic extension?
And how do I use $$f(t+2\pi)=f(t)$$

You have [itex]f(t)=2\pi t-t^2[/tex] in the interval (0,2pi) and you want to extend it in a periodic even "extension" to the negative t-axis from (-2pi,0). So wouldn't f(-t)=f(t) in (-2pi,0) for it to be even? So what happens if you just take the mirror-image of f(t) across the y-axis? What would that give you? But then that "extension" is not $f(t)=2\pi t-t^2$ right? What is the equation of that curve? Likewise, to extend it to the interval (2pi,4pi) in an even manner so that f(2pi+t)=f(t), wouldn't you just reflect it again across the line y=2pi? What then is the equation of that curve in (2pi,4pi)? Then the periodic even extension is just a continuation of those reflections.<br /> <br /> Not sure though what you want to do with that in regards to the DE.[/itex]

 

[frozenguy]

Hey thanks jackmell!
Well hmm..
Thats going to take me a while to absorb..

I started working on this other problem of the same type. One I think that is more applicable to our class.

Could someone please let me know if I have done it correctly so far? It said assume the function to be odd when f(t) is extended to the negative t-axis in a periodic manner.
If I'm right up to where I ended, I got stuck when I have to substitute x_p(t) into my resulting diff eq. How do I go about doing that?

Also is my graph right? Minus the extension?

 

[vela]

Solve the equation x''+10x = sin nt and then use the principle of superposition to write down the solution for the given f(t).

 

[frozenguy]

Solve the equation x''+10x = sin nt and then use the principle of superposition to write down the solution for the given f(t).

Hey vela, thanks for stopping in. Did I do this right?
So I solved for x''+10x=sin(nt) and got $$C_{1}e^{\sqrt{10}t}+C_{2}e^{-\sqrt{10}t}+\frac{1}{10-n^{2}}sin(nt)$$

Considering I did that right, how do I use the principle of superposition?

 

[vela]

You don't need the homogeneous part of the solution. You can tack that on at the very end if needed.

Suppose x''+10x = f(t) has solution x₁(t), and x''+10x = g(t) has solution x₂(t). Using the principle of superposition, you know the solution to x''+10x = f(t)+g(t) is just x(t) = x₁(t)+x₂(t).

 

[jackmell]

Ok guys. Thanks. Now I know what you guys are doing. Never done that before with an ODE. So you're expanding the forcing term in terms of a Fourier series, then solving the DE for each term, then using the Principle of Superposition to then add up all the terms to come up with a single particular solution. Nice! I do have some suggestions though. First, I would simplify the Fourier series for the forcing term f(t):

$$f(t)=\frac{20}{\pi}\sum_{n=0}^{\infty}\frac{1}{2n+1}\sin[(2n+1)t]$$

Ok, so now we have the DE:

$$x''+10x=\frac{20}{\pi}\sum_{n=0}^{\infty}\frac{1}{2n+1}\sin[(2n+1)t]$$

But by the principle of superposition, we can just solve:

$$x''+10x=k\sin(at),\quad k=\frac{20}{\pi(2n+1)},\quad a=2n+1$$

Now, I just solved that in Mathematica cus' it's not my class that I should be solving it manually. But I get:

$$x_p(t)=\frac{-k \text{Cos}\left[\sqrt{10} t\right]^2 \text{Sin}[a t]-k \text{Sin}\left[\sqrt{10} t\right]^2 \text{Sin}[a t]}{-10+a^2}$$

so that the solution for the original problem then becomes:

$$x_p(t)=\sum_{n=0}^{\infty}\frac{-k \text{Cos}\left[\sqrt{10} t\right]^2 \text{Sin}[a t]-k \text{Sin}\left[\sqrt{10} t\right]^2 \text{Sin}[a t]}{-10+a^2},\quad k=\frac{20}{\pi(2n+1)},\quad a=2n+1$$

Is that helping too much guys? I think maybe he may be having problems with this part and hopefully this would help him understand it.

Also, here's something fun if you want. See if you can follow this Mathematica code then try and adapt it to the original problem you had with f(t)=2t-t^2:

myf[t_] := (20/Pi)*Sum[(1/(2*n + 1))*
     Sin[(2*n + 1)*t], {n, 0, 20}]
     
myval = 
  (x /. First[
     DSolve[Derivative[2][x][t] + 
         10*x[t] == k*Sin[a*t], x, t] /. 
      {C[1] -> 0, C[2] -> 0}])[t]
      
myp[t_, n_] := myval /. 
    {k -> 20/(Pi*(2*n + 1)), 
     a -> 2*n + 1}; 
     
mysol[t_] := Sum[myp[t, n], {n, 0, 20}]

Plot[N[D[mysol[t], {t, 2}] + 
     10*mysol[t] - myf[t]] /. t -> tval, 
  {tval, 0, 2*Pi}]

 

[frozenguy]

You don't need the homogeneous part of the solution. You can tack that on at the very end if needed.

The homogeneous part as in $$\frac{1}{10-n^{2}}sin(nt)$$?

Suppose x''+10x = f(t) has solution x₁(t), and x''+10x = g(t) has solution x₂(t). Using the principle of superposition, you know the solution to x''+10x = f(t)+g(t) is just x(t) = x₁(t)+x₂(t).

Hm.. Well I don't have a g(t) in this case do I? Unless the piecewise aspect of f(t) makes a g(t)?

So are you saying the solution $$x=C_{1}e^{\sqrt{10}t}+C_{2}e^{-\sqrt{10}t}$$ is equal to sum of other solutions x1, x2,...? And so what do I do with that?

 

[vela]

The homogeneous part as in $$\frac{1}{10-n^{2}}sin(nt)$$?

No, the homogeneous solution is the solution to x''+10x = 0.

Hm.. Well I don't have a g(t) in this case do I? Unless the piecewise aspect of f(t) makes a g(t)?

No, you've completely missed the point. The idea is if the forcing function is a sum of terms, you can find the response of the system to each term separately and then add those responses together to find the total response of the system.

So are you saying the solution $$x=C_{1}e^{\sqrt{10}t}+C_{2}e^{-\sqrt{10}t}$$ is equal to sum of other solutions x1, x2,...? And so what do I do with that?

 

[frozenguy]

No, the homogeneous solution is the solution to x''+10x = 0.

Ok so the solution is $$C_{1}cos\sqrt{10}x + C_{2}sin\sqrt{10}x$$

No, you've completely missed the point. The idea is if the forcing function is a sum of terms, you can find the response of the system to each term separately and then add those responses together to find the total response of the system.

But in this case it isn't a sum of terms, its just f(t), a piecewise function yeah?

I guess I'm just confused about what I'm doing now. I thought I was substituting xp(t) into the equation above it (the last picture I posted, at the bottom).

 

[vela]

But in this case it isn't a sum of terms, its just f(t), a piecewise function yeah?

The first part of the problem was express f(t) as a Fourier series, which is a sum.

I guess I'm just confused about what I'm doing now. I thought I was substituting xp(t) into the equation above it (the last picture I posted, at the bottom).

Oh, sorry, I missed what you wrote earlier. You can also solve the problem that way. Just plug the series into the differential equation:

$$\frac{d^2}{dx^2}\left(\sum_{n=1}^\infty B_n \sin nt\right) + 10\left(\sum_{n=1}^\infty B_n \sin nt\right) = \frac{10}{\pi} \sum_{n=1}^\infty \frac{1-(-1)^n}{n}\sin nt$$

Differentiate the series twice, term by term, and then collect terms. The coefficient of sin nt on the lefthand side has to match up with the coefficient of sin nt on the righthand side, allowing you to solve for B_n.

 

[frozenguy]

The first part of the problem was express f(t) as a Fourier series, which is a sum.

Oh, sorry, I missed what you wrote earlier. You can also solve the problem that way. Just plug the series into the differential equation:

$$\frac{d^2}{dx^2}\left(\sum_{n=1}^\infty B_n \sin nt\right) + 10\left(\sum_{n=1}^\infty B_n \sin nt\right) = \frac{10}{\pi} \sum_{n=1}^\infty \frac{1-(-1)^n}{n}\sin nt$$

Differentiate the series twice, term by term, and then collect terms. The coefficient of sin nt on the lefthand side has to match up with the coefficient of sin nt on the righthand side, allowing you to solve for B_n.

So if this is right, I'm not completely sure how to add these. I know how to add power series, but I don't think these are power series..
$$\sum^{\infty}_{n=3}\left((-n^{2})B_{n}sin(nt)\right)+10\sum^{\infty}_{n=1}\left(B_{n}sin(nt)\right)=\frac{10}{\pi}\sum^{\infty}_{n=1}\left(\frac{1-(-1)^{n}}{n}sin(nt)\right)$$

 

[vela]

Why did you change the first summation from n=1 to n=3? The n=1 and n=2 terms don't drop out when you differentiate them twice.

 

[frozenguy]

Why did you change the first summation from n=1 to n=3? The n=1 and n=2 terms don't drop out when you differentiate them twice.

I went back to power series to double check how to differentiate them and I don't think I can do that here. Or I did that wrong too haha.

So when differentiating that first series twice, it should be what I wrote but starting at n=1

And these don't look like like they will match up to the right side..

 

[vela]

Now write the LHS has one summation.

 

[frozenguy]

Now write the LHS has one summation.

$$\sum^{\infty}_{n=1}\left(B_{n} (10-n^{2}) sin(nt)\right)$$

But I don't see how this can match the other side.