saad87
- 83
- 0
Hi,
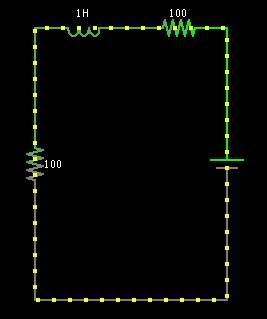
I have the above the circuit and I've ended up with the following differential equation. I've tried solving it by separating the variables, but am not sure if its the right answer.
IR + L(di/dt) + IR = x(t)
x(t) = 5V. But since IR = y(t) and di/dt = 1/R dy/dt.
y(t) is the Voltage across the 2nd Resistor.
y(t) + L/2R(dy/dt) = 2.5
Solution:
y(t) = 2.5 - e(-2*R*t)/L
y(t) is the voltage across the 2nd Resistor.
I've tried simulating it using an online applet, and I've not been getting the predicted result. Any help? How do I analyze this?
I have the above the circuit and I've ended up with the following differential equation. I've tried solving it by separating the variables, but am not sure if its the right answer.
IR + L(di/dt) + IR = x(t)
x(t) = 5V. But since IR = y(t) and di/dt = 1/R dy/dt.
y(t) is the Voltage across the 2nd Resistor.
y(t) + L/2R(dy/dt) = 2.5
Solution:
y(t) = 2.5 - e(-2*R*t)/L
y(t) is the voltage across the 2nd Resistor.
I've tried simulating it using an online applet, and I've not been getting the predicted result. Any help? How do I analyze this?