0aNoMaLi7
Kinematic Range Problem Help!
This problem is kicking my butt...
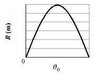
A ball is to be shot from level ground with a certain speed. The figure attached shows the range R it will have versus the launch angle 'theta'at which it can be launched. (The vertical axis is marked in increments of 20.0 m.) The choice of 'theta' determines the flight time. Let tmax represent the maximum flight time in seconds. What is the least speed the ball will have during its flight if 'theta' is chosen such that the flight time is 0.200tmax?
This problem is way too theoretical for me. I know that max range for a projectile is 45 degrees as dictated by the equation R= (V^2/g) x sin2'theta'. I could really use some direction. Thanks. This place rocks! I have told many of my classmates.
This problem is kicking my butt...
A ball is to be shot from level ground with a certain speed. The figure attached shows the range R it will have versus the launch angle 'theta'at which it can be launched. (The vertical axis is marked in increments of 20.0 m.) The choice of 'theta' determines the flight time. Let tmax represent the maximum flight time in seconds. What is the least speed the ball will have during its flight if 'theta' is chosen such that the flight time is 0.200tmax?
This problem is way too theoretical for me. I know that max range for a projectile is 45 degrees as dictated by the equation R= (V^2/g) x sin2'theta'. I could really use some direction. Thanks. This place rocks! I have told many of my classmates.
Attachments
Last edited by a moderator: