Difficult time with motion graphs & dynamics

AI Thread Summary
The discussion focuses on solving a physics problem involving motion graphs and dynamics related to a chin-up exercise. The user initially calculated the acceleration at 1.6 seconds as -60 m/s² and attempted to apply Newton's second law to find the force exerted by the chin-up bar. However, they later realized that their acceleration value was incorrectly converted from cm/s to m/s, which led to an erroneous force calculation. This highlights the importance of unit conversion in physics problems. The user corrected their mistake, indicating a learning moment in the process of solving dynamics problems.
devilish_wit
Messages
16
Reaction score
0

Homework Statement


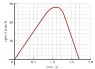
The figure below shows the speed of a person's body as he does a chin-up. Assume the motion is vertical and the mass of the person's body is 72.7 kg. Determine the force exerted by the chin-up bar on his body at the following times.

5-p-041.gif


My answers:

upload_2018-10-8_15-29-4.png

Homework Equations


F = ma

The Attempt at a Solution


I'm not quite sure how to solve that last part:

I solved for the acceleration at 1.6s which is -60m/s^2.

F = ma
-mg + T = m a
T = 72.7kg(60m/s^2) + (9.8m/s^2)(72.7kg)
T = 3649.54?? (this one's wrong)
 

Attachments

  • upload_2018-10-8_15-29-4.png
    upload_2018-10-8_15-29-4.png
    10.9 KB · Views: 844
  • 5-p-041.gif
    5-p-041.gif
    8.5 KB · Views: 818
Physics news on Phys.org
oh never mind guys, I realized I made a stupid mistake. My acceleration was in cm/s and not in m/s!
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Plotting the graph of Friction Force vs. time (Laws of motion)
Replies
1
Views
2K
Analyse motion of an oscillator: x(t)=0.2cos(12*pi*t)
Replies
5
Views
1K
Is it friction or tension acting on the person hanging on a rope?
Replies
4
Views
1K
Distance-time graph of a ball throw vertically up from a fixed point
Replies
5
Views
2K
A 4kg mass sits on a frictionless table....
Replies
3
Views
2K
Atwood's with a cylinder - Rotational Motion
Replies
13
Views
855
Rotational dynamics: Resolving forces
Replies
29
Views
4K
Velocity-time graph given. Plot acceleration vs time etc.
Replies
1
Views
8K
Projectile Motion Graph Analysis
Replies
1
Views
2K
Why does this not work? Projectile Motion problem for Dynamics Class
Replies
19
Views
3K

Hot Threads

Recent Insights

Back
Top