SUMMARY
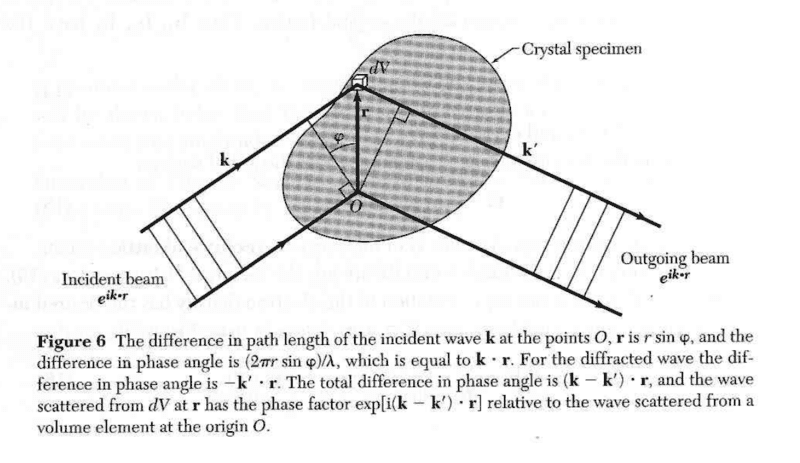
The discussion focuses on the diffraction condition as presented in Kittle's "Introduction to Solid State Physics." The key point is the distinction between the phase difference for the incident wave, which is positive, and the phase difference for the diffracted wave, which is negative. This is explained through the equations \(\mathbf{k} \cdot \mathbf{r} > 0\) and \(\mathbf{k'} \cdot \mathbf{r} < 0\), indicating that the phase of the incident wave advances positively until reflection, while the phase of the diffracted wave requires a sign inversion post-reflection to accurately represent the full phase difference.
PREREQUISITES
- Understanding of wave vectors in solid state physics
- Familiarity with phase differences in wave mechanics
- Knowledge of reflection principles in physics
- Basic grasp of Kittle's "Introduction to Solid State Physics"
NEXT STEPS
- Review the section on wave vectors in Kittle's "Introduction to Solid State Physics"
- Study the mathematical derivation of phase differences in wave mechanics
- Explore the concept of diffraction and its applications in solid state physics
- Examine examples of reflection and phase inversion in wave phenomena
USEFUL FOR
Students and educators in physics, particularly those studying solid state physics, as well as researchers interested in wave mechanics and diffraction phenomena.