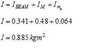Dimension analysis problem for Vibration Experiment

[DARK_STALKER]

1.I am busy with an assignment based on a Vibration experiment in a Mechanical Engineering degree program The procedure is documented in the lab handout and one part is to compare the measured natural frequency to the calculated natural frequency The formula given in the handout for natural frequency is given by wn = sqrroot of (K theta / I)

2.This is where I am getting confused as I know omega is supposed to be in Rad/s but if I do dimensional analysis on this formula i get it in 1/s which is = Hz. The lecturer tells me my analysis is incorrect which it probably is but could someone please explain where i am going wrong. He is saying the result of the equation is in Rad/s and must be divided by 2 Pi still to get to Hz

3. I have attached a Jpeg of my attempt at his problem

 

[tiny-tim]

Welcome to PF!

Hi DARK_STALKER! Welcome to PF!

(have an omega: ω and a pi: π and a theta: θ )

… I know omega is supposed to be in Rad/s but if I do dimensional analysis on this formula i get it in 1/s which is = Hz.

radians are dimensionless …

1 rad/s does have dimensions of 1/T.

 

[DARK_STALKER]

Thanks tiny-tim... I see the are no units in the numerator of my dimension analysis and of course Radians are dimensionless was only thinking of units of Hz /s.

Is my analysis correct though as I got 1/s

I know rads*1 = rads

How do the rads get into the result or is it the fact that because the numerator is one you could really apply it to anything /s

Thanks

 

[tiny-tim]

Hi DARK_STALKER!

Is my analysis correct though as I got 1/s

Yes.

I'm afraid dimensional analysis doesn't solve everything, and radians just don't show up on the "radar"!