lapantufla
- 3
- 0
- Homework Statement
- Show that if the charge (or current) distribution has axial symmetry then the electric (or magnetic) dipole moment is null.
Show that the quadrupole moments Qij with i different from j are null under the same conditions.
- Relevant Equations
- Electric Dipole Moment Equation.
Magnetic Dipole Moment Equation.
Quadrupole Moment Equation.
Hello, I would like to find a mathematical demonstration of this problem. While I have always used it, I could never prove it. Given a charge or current distribution with axial symmetry the electric and magnetic dipole moment are null:
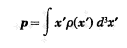 (electric dipole moment)
(electric dipole moment)
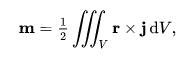 (magnetic dipole moment)and that the elements outside the diagonal of the quadrupole moment are also canceled:
(magnetic dipole moment)and that the elements outside the diagonal of the quadrupole moment are also canceled:
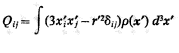 (Quadrupole moment)From already thank you very much. (excuse my English, I use a translator).
(Quadrupole moment)From already thank you very much. (excuse my English, I use a translator).
 !
!