- #1
SpookyMulder
- 6
- 0
Hi, I'm reading Schwartz's book "Quantum field theory and the standard model", section 7.3.2., page 95 (https://books.google.com/books?id=H...ce=gbs_ge_summary_r&cad=0#v=onepage&q&f=false)
where he's talking about disconnected diagrams, the ones that have subsets of external vertices connected to each other without interacting with the other subsets. Schwartz basically states that the disconnected part of the [itex]S[/itex]-matrix (or is he talking about the full [itex]S[/itex]-matrix here, please correct me if I'm wrong) factorizes into the products of the two [itex]1\to3[/itex] connected processes. Then he says that the connected diagram has only single overall delta-function [itex]\delta^4(\sum p)[/itex] (and cannot produce more delta-functions which is related to the cluster decomposition principle), while the disconnected matrix elements will have extra delta-functions [itex]\mathcal{M}=\delta^4(\sum_{subset} p)(\dots)[/itex].
Finally, he states that disconnected amplitudes are always infinitely larger than the connected ones, so that the interference between connected and disconnected diagrams vanishes. Now, what does it mean that there's no interference? Does it mean that [itex]\left|\mathcal{M}_{disc}+\mathcal{M}_{conn}\right|^2 = \left|\mathcal{M}_{disc}\right|^2+\left|\mathcal{M}_{conn}\right|^2 [/itex] or something else? How do we prove it in general? I know I should read Weinberg at some point, but still...
Schwartz also has a problem (7.2) at the end of the chapter related to this discussion (see page 103 https://books.google.com/books?id=H...ce=gbs_ge_summary_r&cad=0#v=onepage&q&f=false)
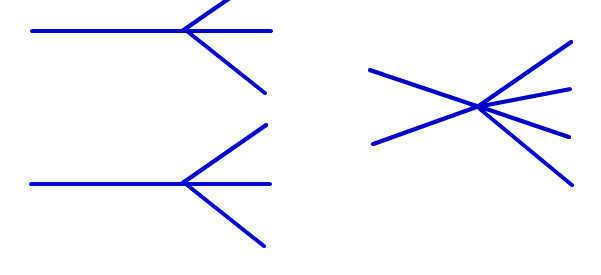
Attached are the relevant diagrams. Using position-space Feynman rules, I calculated
[tex]\langle i|S| \rangle_{conn} = i \lambda (2\pi)^4 \delta^{4}(p_1+p_2-p_3-p_4-p_5-p_6)[/tex]
[tex]\langle i|S| \rangle_{disc} = -g^2 (2\pi)^8 \delta^{4}(p_1-p_3-p_4) \delta^{4}(p_2-p_5-p_6)[/tex]
where [itex]p_1, p_2[/itex] --- incoming, [itex]p_3, p_4,p_5,p_6[/itex] --- outgoing momenta.
How do I show that there's no interference?
where he's talking about disconnected diagrams, the ones that have subsets of external vertices connected to each other without interacting with the other subsets. Schwartz basically states that the disconnected part of the [itex]S[/itex]-matrix (or is he talking about the full [itex]S[/itex]-matrix here, please correct me if I'm wrong) factorizes into the products of the two [itex]1\to3[/itex] connected processes. Then he says that the connected diagram has only single overall delta-function [itex]\delta^4(\sum p)[/itex] (and cannot produce more delta-functions which is related to the cluster decomposition principle), while the disconnected matrix elements will have extra delta-functions [itex]\mathcal{M}=\delta^4(\sum_{subset} p)(\dots)[/itex].
Finally, he states that disconnected amplitudes are always infinitely larger than the connected ones, so that the interference between connected and disconnected diagrams vanishes. Now, what does it mean that there's no interference? Does it mean that [itex]\left|\mathcal{M}_{disc}+\mathcal{M}_{conn}\right|^2 = \left|\mathcal{M}_{disc}\right|^2+\left|\mathcal{M}_{conn}\right|^2 [/itex] or something else? How do we prove it in general? I know I should read Weinberg at some point, but still...
Schwartz also has a problem (7.2) at the end of the chapter related to this discussion (see page 103 https://books.google.com/books?id=H...ce=gbs_ge_summary_r&cad=0#v=onepage&q&f=false)
Calculate the contribution to [itex]2 \to 4[/itex] scattering from the Lagrangian [itex]\mathcal{L} = -\frac{1}{2} \phi \Box \phi + \frac{g}{3!}\phi^3 + \frac{\lambda}{6!}\phi^6[/itex] from the connected diagram, with the 6-point vertex, and the disconnected diagram with the 3-point vertex. Show that there is no interference. (There are of course many connected diagrams with the 3-point vertex that you can ignore).
Attached are the relevant diagrams. Using position-space Feynman rules, I calculated
[tex]\langle i|S| \rangle_{conn} = i \lambda (2\pi)^4 \delta^{4}(p_1+p_2-p_3-p_4-p_5-p_6)[/tex]
[tex]\langle i|S| \rangle_{disc} = -g^2 (2\pi)^8 \delta^{4}(p_1-p_3-p_4) \delta^{4}(p_2-p_5-p_6)[/tex]
where [itex]p_1, p_2[/itex] --- incoming, [itex]p_3, p_4,p_5,p_6[/itex] --- outgoing momenta.
How do I show that there's no interference?
Last edited: