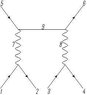
- #1
Thor Shen
- 17
- 0
the number stand for the index of particles (quarks and gluons)
[itex]M=\bar{v}(p_2) ig_sT_{12}\gamma^\mu(12)u(p_1)\frac{-i}{p_7^2}\bar{u}(p_5) ig_sT_{56}\gamma_\mu(56)\bar{v}(p_6)\frac{-i}{m-\gamma^\mu p_{9\mu}}\bar{v}(p_3) ig_sT_{34}\gamma^\mu(34)u(p_4)\frac{-i}{p_8^2}\bar{u}(p_5)ig_sT_{56}\gamma_\mu(56)\bar{v}(p_6)[/itex]
[itex]u(p_i)[/itex] and [itex]v(p_i)[/itex] stand for the wave function of quark and antiquark, respectively. [itex]p_i[/itex] stand for the four momentum
I am studying the QCD right now. Do I write the amplitude above right?
Someone recommend me a textbook by T.Muta. But I make some confusion when I confront complex diagrams like above. Which book or paper can tell me about this? Thank you!
Attachments
Last edited: