Displacement of Hanging Mass - Simple Pulley System

[erobz]

I'm having some kind of mental block.

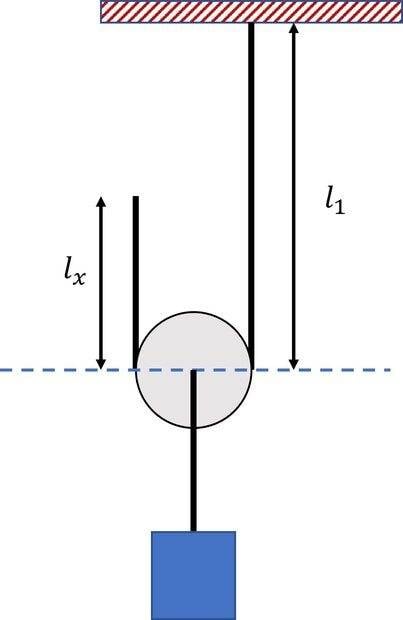
If I extend $l_x$ by $\delta$ ,I expect the hanging mass to move $\frac{ \delta}{2}$.

I can't figure out how this is the case from the constraint:

$$ l_x+l_1=C $$

$C$ is an arbitrary length

I keep getting that $l_1$ changes by $\delta$, but that must mean the height of the mass changes by $\delta$...

 

[PeroK]

I suspect you need to differentiate between the distance you pull the left hand cord up, $\delta$, and the increase in distance from that point to the pulley, $\frac \delta 2$.

 

[vanhees71]

Call the distance of the left end of the cord from the ceiling $y$. Then $l_x=l_1-y$ and $l_x=C-l_1$ from the constraint given by the fixed length of the entire cord. Then you can eliminate the somewhat inconvenient quantity $l_1$ in favor of $y$ which has a well defined meaning of a coordinate, i.e., it's a length measured from a fixed reference point (the ceiling):
$$C-l_1=l_1-y \; \Rightarrow \; L_1=\frac{1}{2}(C+y).$$
So if you change $y$ by $\delta$ (which is the same as changing $l_x$ by $-\delta$) $L_1$ (the distance of the pulley from the ceiling) changes by $\delta/2$.

 

[erobz]

Then you can eliminate the somewhat inconvenient quantity $l_1$ in favor of $y$ which has a well defined meaning of a coordinate, i.e., it's a length measured from a fixed reference point (the ceiling):

The addition of the coordinate $y$ and the weirdness seems to vanish right in front of my eyes. Amazing!

 

[erobz]

My key failure was that I had not defined a fixed coordinate system. I basically was trying to measure distances relative the datum at the center of the pulley...a transformation not so obvious to me.