Noname
- 1
- 0
Member has been warned not to remove the template.
Hi guys,
Consider a circular capacitor with a disk of radius a and plate separation d, as shown in the figure below. Assuming the capacitor is filled with a dielectric constant epsilon and the capacitor is fed by a time harmonic current I0
(a) Find the magnetic field distribution inside the capacitor assuming that the electric field is constant.
(b) Compute the complex Poynting vector and prove that the capacitor does not radiate an electromagnetic field. (Hint: S=(1/2)ExH ; only Re[S ] radiates an electromagnetic field.)
(c) Compute the total stored energy density W and show that far away from the center (kr<< 1): grad(S)-iwW = 0
(d) Find the surface current density as a function of radial distance on the top plate.
I don't really know how to do the (b). I have S=(1/2)ExH. I think I need to write E and H in complex, I have E=Eo*exp(iwt) and H=Ho*exp(iwt). But I can't prove S is only an imaginary part.
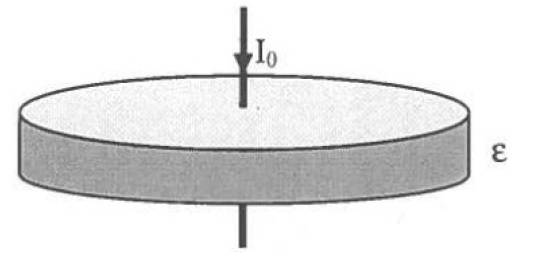
Consider a circular capacitor with a disk of radius a and plate separation d, as shown in the figure below. Assuming the capacitor is filled with a dielectric constant epsilon and the capacitor is fed by a time harmonic current I0
(a) Find the magnetic field distribution inside the capacitor assuming that the electric field is constant.
(b) Compute the complex Poynting vector and prove that the capacitor does not radiate an electromagnetic field. (Hint: S=(1/2)ExH ; only Re[S ] radiates an electromagnetic field.)
(c) Compute the total stored energy density W and show that far away from the center (kr<< 1): grad(S)-iwW = 0
(d) Find the surface current density as a function of radial distance on the top plate.
I don't really know how to do the (b). I have S=(1/2)ExH. I think I need to write E and H in complex, I have E=Eo*exp(iwt) and H=Ho*exp(iwt). But I can't prove S is only an imaginary part.