Electric field in a capacitor with a dielectric

[Granger]

Homework Statement

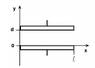
A parallel plate capacitor has 2 square plates of side l, separated by a distance d (l is a lot bigger than d). Between the plates, there is a linear and non-homogeneous dielectric with constant $$\epsilon_R=1+ay$$ with $$a$$a positive constant. Calculate the electric field between the plates knowing that the capacitor is connected to a battery of voltage V (positive armor at y=0).

Here's an image to help understanding the geometry of the problem:

Homework Equations

Gauss Law:
$$\oint_S {E_n dA = \frac{1}{{\varepsilon _0 }}} Q_{inside}$$

Generalized Gauss law:
\oint_S {D_n dA = Q_{inside free}$$

$$D=\epsilon E$$

The Attempt at a Solution

So first what I thought was that because the capacitor is connected to a battery we will have a an accumulated charge $$+Q$$ in the positive armor and $$-Q$$ in the negative armor-
Now in a capacitor with the empty space between the plates, the electric field is $$E=\frac{Q}{\epsilon*A}$$ adapting to our capacitor $$E=\frac{Q}{(1+ay)\epsilon*l^2}$$.

Now I thought I was done, but my textbook provided a different answer

$$E=\frac{Va}{(1+ay)\log{1+ad}}$$

Now I have no idea on how to relate my expression to the expression I got. I know there is probably a relation between Voltage V and the charge Q and that's probably how I will eliminate the $$\epsilon_0$$. I also know that 1+ad is the constant in the upper plate. But how do I include it in the field? Why do you have a logarithm?
Can someone help me please?
Thanks!

 

[kuruman]

Consider a slice of thickness dy. Find its capacitance dC. Add up all slices dC (they are capacitors in series) by integrating.

 

[Granger]

Consider a slice of thickness dy. Find its capacitance dC. Add up all slices dC (they are capacitors in series) by integrating.

Sorry could you elaborate more please.

 

[kuruman]

Consider the space between the plates as being stacked capacitors in series. Consider one of them having "plate" separation dy at distance y from the bottom plate. Find an expression of its capacitance dC. Now you want the entire capacitance of all those capacitors in series that make up the space between the plates. Add them up as you would for capacitors in series, but you need to an integral. This will give the capacitance C. Knowing C, you can find the charge Q on the plates that the battery put on. Knowing Q you can find E between the plates. Whatever you do, don't assume that the field is uniform between the plates, so V = Ed does not work here but Q = CV is always valid.

 

[Granger]

Consider the space between the plates as being stacked capacitors in series. Consider one of them having "plate" separation dy at distance y from the bottom plate. Find an expression of its capacitance dC. Now you want the entire capacitance of all those capacitors in series that make up the space between the plates. Add them up as you would for capacitors in series, but you need to an integral. This will give the capacitance C. Knowing C, you can find the charge Q on the plates that the battery put on. Knowing Q you can find E between the plates. Whatever you do, don't assume that the field is uniform between the plates, so V = Ed does not work here but Q = CV is always valid.

But won't my expression then depend on C? The question that follows this problem es exactly to determine the capacity. So there must be an alternative way to proceed in this?.
However based on what you said I remembered the fact that D is uniform across the capacitor and $$D=\sigma$$. That means that we will have

$$E=\frac{\sigma}{\epsilon_0(1+ay)}$$

Now because $$V=\int_{0}^{d} E dy$$ we get to $$V=\frac{\sigma}{\epsilon_0 a}\log(1+ad)$$

Isolating $$\sigma$$ and substituting in the equation for E we get to the expression asked.

 

[kuruman]

But won't my expression then depend on C?

In what way? C is a geometric quantity and depends on the plate dimensions, plate separation and the parameters specifying the dielectric. This is also true for the electric field, the voltage and the charge on the plates. All these quantities can be cast in terms of the given parameters.

So there must be an alternative way to proceed in this?.

There is and I outlined it in post #3. You can first find the capacitance and then the electric field or the other way around. You picked the "other way around."