Does a rotating loop in a magnetic field induce emf without cutting field lines?

[cnh1995]

When a loop rotates in a magnetic field, does it have to actually "cut" the field lines in order to have emf induced in it? I mean if the loop is rotating and there is a rate of change of flux in the loop, does this mean that the loop is also "cutting" the field lines? I know if the loop is cutting the field lines, there is a change of flux associated with it at the same time such that motional emf BlvsinΘ= induced emf dΦ/dt.

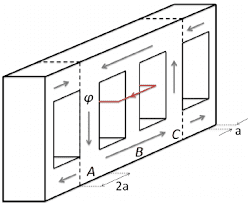
Consider the middle limb. Suppose it is excited by a dc source and a constant flux is enclosed in the core and no flux is present in the air. Now consider the red loop on the middle limb. If it is tilted at an angle Θ, the flux linking with the loop will change since flux Φ=BAcosΘ. But the loop will not physically "cut" the field lines. Will there be emf induced in the loop if it moves but doesn't physically "cut" the field lines? There is a change in flux associated with the loop but is that sufficient to induce emf in the loop?

 

[Khashishi]

Your diagram is confusing, but I'm going to guess what you are struggling with. It looks like your diagram shows B and A, but you mean something completely different by B and A in your equation Φ=BAcosΘ.
The magnetic field is a vector quantity. The flux is the sum over the component of the magnetic field which is perpendicular to your surface. If you angle the loop so it is not perpendicular to the magnetic field, then the area of the surface intersecting the core increases, but the field is no longer perpendicular to the surface, so the contribution at each point in the intersection is smaller. The effects cancel out and the total flux is the same.

 

[cnh1995]

Your diagram is confusing, but I'm going to guess what you are struggling with. It looks like your diagram shows B and A, but you mean something completely different by B and A in your equation Φ=BAcosΘ.
The magnetic field is a vector quantity. The flux is the sum over the component of the magnetic field which is perpendicular to your surface. If you angle the loop so it is not perpendicular to the magnetic field, then the area of the surface intersecting the core increases, but the field is no longer perpendicular to the surface, so the contribution at each point in the intersection is smaller. The effects cancel out and the total flux is the same.

So if a conductor is moving in a magnetic field, the physical cause of emf induced in it is always "motional emf" even though it can be written as dΦ/dt. This is intuitive so far. My question in the OP stems from a recent thread of mine in the EE forum regarding dc machine magnetics.
https://www.physicsforums.com/threads/dc-machine-magnetics.881877/
You can see that the iron rotor rotates but doesn't physically cut the flux since most of the flux is in the rotor iron teeth because of the difference in reluctances (see #5 and #6). Now, there is a change of flux associated with the armature coils but they don't physically cut most of the flux lines because the flux is crowded in the rotor iron teeth, and yet there is an induced emf in the armature conductors as if they cut all the flux. Isn't it paradoxial? Or am I missing something obvious?