qijiongli
- 3
- 0
If not, then what are the conditions for us to construct a periodic boundary condition(PBC)?
If so, then please help me construct a PBC for the lattice shape in the attachments.
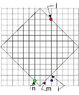
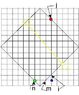
I want to ask that what lattice site m's left neighbor is and what lattice site i's down neighbor is.From the picture, both m's left and i's down neighbor is the BLUE site, but in the PBC, the neighbors are GREEN and RED correspondingly (right?). However, the GREEN site and the RED site are impossible to be the same site in the PBC(right?). So I'm confused with it.
thanks a lot
If so, then please help me construct a PBC for the lattice shape in the attachments.
I want to ask that what lattice site m's left neighbor is and what lattice site i's down neighbor is.From the picture, both m's left and i's down neighbor is the BLUE site, but in the PBC, the neighbors are GREEN and RED correspondingly (right?). However, the GREEN site and the RED site are impossible to be the same site in the PBC(right?). So I'm confused with it.
thanks a lot