lillybeans
- 67
- 1
A question in my textbook made me think:
A spool of wire of mass M and radius R resting on some surface is unwound under a constant force F. Assume the spool is a uniform solid cylinder that doesn't slip, show that a) the acceleration of the center of mass is 4F/3M and b) the force of friction is to the right and equal in magnitude to F/3.
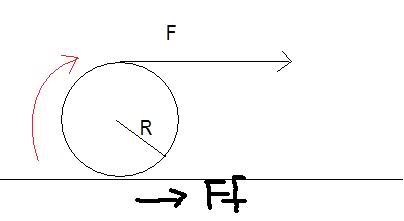
I solved both part a) and b) correctly, but now a contradiction arises.
in part a), I set: Tf=Ia, where Tf is the torque generated by F. So I wrote (RF=Ia, then solved from there.) But now I'm wondering why did I get the right answer when I didn't include the torque caused by friction in the opposite direction. Clearly, there is friction, or otherwise the thing would be slipping. If there is friction, it would produce a torque in the counterclockwise direction, no? so for net torque, shouldn't I have written:
Tnet= Tf-TFf=Ia instead of Tf=Ia? But if I do that, I won't get the right answer!
So if part A is solved without friction, why are they asking for force of friction in part B? isn't that kind of strange that in part a) we assume friction produce no negative torque but in part b) it impedes the motion? In part b) I wrote "F-Ff=ma" and solved from there. Why do we not include torque caused by friction in part A when solving for net torque?
In fact, when do we EVER include torque caused by friction in the calculation of these problems? Am I double counting friction here?
A spool of wire of mass M and radius R resting on some surface is unwound under a constant force F. Assume the spool is a uniform solid cylinder that doesn't slip, show that a) the acceleration of the center of mass is 4F/3M and b) the force of friction is to the right and equal in magnitude to F/3.
I solved both part a) and b) correctly, but now a contradiction arises.
in part a), I set: Tf=Ia, where Tf is the torque generated by F. So I wrote (RF=Ia, then solved from there.) But now I'm wondering why did I get the right answer when I didn't include the torque caused by friction in the opposite direction. Clearly, there is friction, or otherwise the thing would be slipping. If there is friction, it would produce a torque in the counterclockwise direction, no? so for net torque, shouldn't I have written:
Tnet= Tf-TFf=Ia instead of Tf=Ia? But if I do that, I won't get the right answer!
So if part A is solved without friction, why are they asking for force of friction in part B? isn't that kind of strange that in part a) we assume friction produce no negative torque but in part b) it impedes the motion? In part b) I wrote "F-Ff=ma" and solved from there. Why do we not include torque caused by friction in part A when solving for net torque?
In fact, when do we EVER include torque caused by friction in the calculation of these problems? Am I double counting friction here?