Does Point M Lie on Line BC in This Triangle Bisector Problem?

[The legend]

Homework Statement

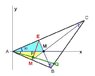
Let ABC be a triangle in which angle A = 60⁰. Let BE and CF be the bisectors of the angles B and C, with E on AC and F on AB. Let M be the reflection of A in the line EF. Prove that M lies on BC.

http://img135.imageshack.us/img135/606/sumu.png

The Attempt at a Solution

I didnt really get this problem...i was led to make assumptions and then solve, but that is wrong, i believe.

So can you please help me out?

 

[The legend]

any help?

 

[zorro]

I asked this question to one of my friends. This is what he replied-

E is equidistant from AB and BC
F is equidistant from AC and BC
Perpendicular from E to AB (EX), perpendicular from F to AC (FY) and perpendicular from A to EF (AZ) are concurrent.
B+C=120°

I could not infer anything from this. May be you can.
Explain me this if you get it

 

[ehild]

Have you got any hint from your teacher?

ehild

 

[The legend]

Have you got any hint from your teacher?

ehild

no, this was actually asked in an olympiad...

 

[The legend]

I asked this question to one of my friends. This is what he replied-

E is equidistant from AB and BC
F is equidistant from AC and BC
Perpendicular from E to AB (EX), perpendicular from F to AC (FY) and perpendicular from A to EF (AZ) are concurrent.
B+C=120°

I could not infer anything from this. May be you can.
Explain me this if you get it

Erm...
I couldn't get it yet..
your friend could solve it?

 

[The legend]

anyone, please?

 

[ehild]

Be patient...

Try this page. http://en.wikipedia.org/wiki/Incircle_and_excircles_of_a_triangle

ehild

 

[The legend]

i'm sorry, but i still did not understand...
Of that page i did already know of Incircles and Excircles and relation to the area, Nine Point Circle theorem. But i did not understand how to apply that property...could you please give be a deeper explanation?

 

[chaoseverlasting]

For an equilateral triangle the solution is simple. The incenter coincides with the circumcenter, orthocenter etc and thus EF is parallel to BC with E and F being the mid points of their respective sides. Thus, the reflection of A from EF will lie on BC and will be the mid point of BC. I'm just thinking of how to prove this for a more general case.

One really long, but general method to prove or disprove this would be to assume that the point A lies on the origin. Let the point B lie on the X axis and its coordinates be (x1,0).

As we know the angle A is 60 degrees, the equation of the line AC comes out to be $$y=\sqrt{3} x$$ and the point C has coordinates $$x_2, \sqrt{3} x_2$$.

The line BE thus has the equation $$y=\frac{1}{\sqrt{3}} x$$.

The long winded part is finding the points of intersection of these two line to get the points E and F, thus to get the equation of EF and to find the reflection of A. If this lies on the x-axis then its proven, otherwise not.

There should be a geometrical solution for this which is much simpler, however, the above solution should also work albeit with a considerable amount of work.

 

[The legend]

For an equilateral triangle the solution is simple. The incenter coincides with the circumcenter, orthocenter etc and thus EF is parallel to BC with E and F being the mid points of their respective sides. Thus, the reflection of A from EF will lie on BC and will be the mid point of BC. I'm just thinking of how to prove this for a more general case.

I could do that too, but as you the general case isn't working out so well.

 

[ehild]

I got it at last. See the picture. Let be β=60-δ and γ=60+δ. The point M is the centre of the incircle. Let be the distance AM=1. Find the angles around M and everywhere in terms of δ, and apply the Sine Law for the yellow and blue triangles to find the lengths AE and AF. Find the coordinates of E and F. Find the tangent of the line EF. Find the angle its normal encloses with the x axis. Find AP and AQ, using the Sine Law again.

ehild

 

[The legend]

I got it at last. See the picture. Let be β=60-δ and γ=60+δ. The point M is the centre of the incircle. Let be the distance AM=1.

ehild

But is doing such an assumption correct?

 

[ehild]

Why not? The mirror image stays on the opposite side if you blow up that triangle. Instead of starting from the sides of the triangle, I start with AM. All the other lengths including the sides of the triangle are proportional to it.

ehild

 

[The legend]

okay, thank you.
This can be generalized too, like taking AM=x.?

 

[ehild]

Of course, you can call it anything. You can express all lengths in terms of this x and delta. All lengths are proportional to this x, which cancels at the end when finding the ratio AQ/AP.

ehild

 

[ehild]

I got it at last. See the picture. Let be β=60-δ and γ=60+δ. The point M is the centre of the incircle. Let be the distance AM=1. Find the angles around M and everywhere in terms of δ, and apply the Sine Law for the yellow and blue triangles to find the lengths AE and AF. Find the coordinates of E and F. Find the tangent of the line EF. Find the angle its normal encloses with the x axis. Find AP and AQ, using the Sine Law again.

ehild

There was a mistake in the figure, it is corrected now.

ehild

 

[The legend]

Here is a solution i found in the answer key.

In the figure : http://img692.imageshack.us/img692/5837/sumo.png

AFIE is cyclic. Circle AFC cut BC at D. (BF. BA)=(BI.BE)=(BD. BC). IDCE is
cyclic, angle EIC = angle EDC=60°.

ABDE is cyclic. AF=FD, AE=ED (angle ACF = angle FCD, Ð ABE = Ð EBD). AFDE is kite.
Thus, D is the mirror of A in EF.

 

[zorro]

(BF. BA)=(BI.BE)=(BD. BC)

Which property is this?