Jeremy1986
- 17
- 3
In deducing the zeroth law of thermodynamics in micro-canonical ensemble, there is a frequently-mentioned example. Suppose we put two isolated system, system 1 and 2, in contact and allowing them to exchange heat.
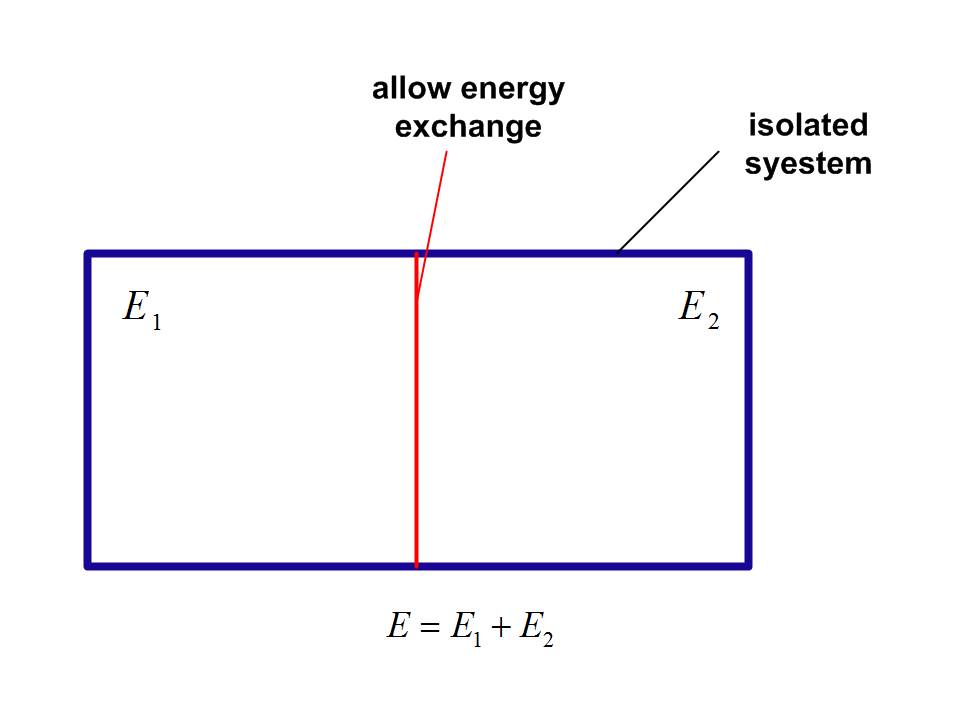 The total energy of the combined system is
The total energy of the combined system is
$$E = {E_1} + {E_2}$$
The total allowed phase space is
$$\Omega (E) = \int d {E_1}{\Omega _1}({E_1}){\Omega _2}(E - {E_1}) = \int d {E_1}\exp [\frac{{{S_1}({E_1}) + {S_2}(E - {E_1})}}{{{k_B}}}]$$
By taking the maximum of the integrand,
$$\frac{{\partial {S_1}({E_1})}}{{\partial E}} + \frac{{\partial {S_2}(E - {E_1})}}{{\partial E}} = 0$$
we get the equilibrium state ##(E_1^{eq},E - E_1^{eq}) ##, which is the macrostate with exponetially larger number of microstates, and also get the equilibrium condition
$$\frac{{\partial {S_1}({E_1})}}{{\partial {E_1}}} = \frac{{\partial {S_2}(E - {E_1})}}{{\partial {E_2}}}$$---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
The equal a priori probability postulate, as descripted by David Tong p4 , is
For an isolated system in equilibrium, all accessible microstates are equally likely.
So my question is, does that mean the microsates corresponds to the equilibrium macrosate ##(E_1^{eq},E - E_1^{eq}) ## possses equal probability or all the microstates with constant ##E ## (the blue line in next figure) possesses equal probability?
For me, it looks like every reference I found indicates the second statement. But for a microsate corresponds to ##(E_1^{0},E - E_1^{0}) ## which is not at equilibrium, does it have the same probability as a microstate of ##(E_1^{eq},E - E_1^{eq}) ##?

$$E = {E_1} + {E_2}$$
The total allowed phase space is
$$\Omega (E) = \int d {E_1}{\Omega _1}({E_1}){\Omega _2}(E - {E_1}) = \int d {E_1}\exp [\frac{{{S_1}({E_1}) + {S_2}(E - {E_1})}}{{{k_B}}}]$$
By taking the maximum of the integrand,
$$\frac{{\partial {S_1}({E_1})}}{{\partial E}} + \frac{{\partial {S_2}(E - {E_1})}}{{\partial E}} = 0$$
we get the equilibrium state ##(E_1^{eq},E - E_1^{eq}) ##, which is the macrostate with exponetially larger number of microstates, and also get the equilibrium condition
$$\frac{{\partial {S_1}({E_1})}}{{\partial {E_1}}} = \frac{{\partial {S_2}(E - {E_1})}}{{\partial {E_2}}}$$---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
The equal a priori probability postulate, as descripted by David Tong p4 , is
For an isolated system in equilibrium, all accessible microstates are equally likely.
So my question is, does that mean the microsates corresponds to the equilibrium macrosate ##(E_1^{eq},E - E_1^{eq}) ## possses equal probability or all the microstates with constant ##E ## (the blue line in next figure) possesses equal probability?
For me, it looks like every reference I found indicates the second statement. But for a microsate corresponds to ##(E_1^{0},E - E_1^{0}) ## which is not at equilibrium, does it have the same probability as a microstate of ##(E_1^{eq},E - E_1^{eq}) ##?
Last edited: