SUMMARY
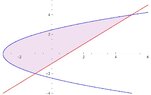
The discussion focuses on evaluating the double integral $\iint_{R} xy \, dA$ over the region $R$ bounded by the line $y = x - 1$ and the parabola $y^2 = 2x + 6$. The iterated integral is established as $I=\int_{-2}^{4} y\int_{\frac{y^2-6}{2}}^{y+1} x\,dx\,dy$, leading to the conclusion that $I=36$. Participants discuss the setup of the integral using horizontal strips and provide insights into the intersection points of the curves involved.
PREREQUISITES
- Understanding of double integrals in calculus
- Knowledge of iterated integrals and their setup
- Familiarity with curves and their intersections
- Ability to apply the quadratic formula for solving polynomials
NEXT STEPS
- Study the method of evaluating double integrals using horizontal and vertical strips
- Learn about the properties of parabolas and linear equations in calculus
- Explore the application of the quadratic formula in finding intersection points of curves
- Investigate advanced techniques for solving double integrals in different coordinate systems
USEFUL FOR
Students and educators in calculus, mathematicians interested in integral calculus, and anyone looking to deepen their understanding of double integrals and region boundaries in multivariable calculus.