- #1
Double Laser Interference: Solving for Small Angles
- Thread starter jegues
- Start date
-
- Tags
- Lasers Single slit Slit
In summary, this conversation is about a problem involving single slit diffraction with two separate lights of different wavelengths. The person asking for help is having trouble finding the distance between a given angle and the distance from the screen to the slit. They are also having trouble understanding where sin(theta) is situated in the problem. Another person suggests looking in a textbook for a standard formula and clarifies that the diffraction patterns are separate and independent of each other. They also provide a resource for understanding the angle and distance in the problem. In the end, it is suggested to use the small angle approximation for easier calculations.
- #2
- 12,180
- 182
Single slit diffraction . . . there is a standard formula for this. Look in your textbook.
- #3
jegues
- 1,097
- 3
Redbelly98 said:
I'm aware but I don't know how to deal with two separate lights at the same time, who's wavelength are different.
Can you clarify that portion?
- #4
ehild
Homework Helper
- 15,542
- 1,917
The diffraction patterns are also separate, independent of each other.
ehild
ehild
- #5
jegues
- 1,097
- 3
ehild said:
I'm still having a really tough time with this problem. All I can identify is that,
[tex]dsin\theta_{r} = m\lambda_{r}[/tex]
and
[tex]dsin\theta_{g} = n\lambda_{g}[/tex]
so,
[tex]m\lambda_{r} = n\lambda_{g}[/tex]
Where m = 3, so n =3.5 therefore the nearest minimum would be at 3 for the green laser.
Now how can I calculate the difference between these two minimum on the screen?
Any help would be greatly appreciated, I'm really lost.
- #6
ehild
Homework Helper
- 15,542
- 1,917
Find the distances from L and sin(theta).
ehild
ehild
- #7
jegues
- 1,097
- 3
ehild said:
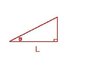
I don't understand where sin(theta) is situated.
I know that L is the distance between the screen and the slit but where is sin(theta)?
Theta is the angle in the triangle like so, correct?
I don't know where sin(theta) is so I'm having trouble finding the distance between that and L.
One could say that sintheta is simply opposite over hypotenuse, but I don't know either of those sides.
Attachments
- #8
ehild
Homework Helper
- 15,542
- 1,917
Theta is the angle of the diffracted beam with respect to the central beam.
See : http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/sinslitd.html#c1
ehild
See : http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/sinslitd.html#c1
ehild
- #9
- 12,180
- 182
Also, at small angles (as occur in this problem), θ, sinθ, and tanθ are all approximately equal to each other.
Last edited:
FAQ: Double Laser Interference: Solving for Small Angles
1. What is a single slit with two lasers?
A single slit with two lasers is an experimental setup in which two lasers are used to produce a diffraction pattern through a single slit. The lasers are typically of different colors or wavelengths, and the resulting pattern is a combination of the two individual patterns.
2. How does a single slit with two lasers work?
In a single slit with two lasers experiment, the lasers are directed towards a single slit. The slit diffracts the light, producing a pattern of bright and dark fringes on a screen placed behind it. The two lasers produce individual patterns, which overlap to create a combined pattern with alternating bright and dark fringes of varying intensity.
3. What is the purpose of using two lasers in a single slit experiment?
The purpose of using two lasers in a single slit experiment is to study the interference patterns produced by the combination of two different wavelengths of light. This allows scientists to better understand the principles of wave interference and diffraction.
4. How is the distance between the two lasers and the slit determined?
The distance between the two lasers and the slit in a single slit experiment is determined by the desired experimental setup. The distance can be adjusted to change the intensity and spacing of the interference pattern on the screen. Typically, the distance is chosen based on the specific wavelengths of the lasers being used.
5. What are the applications of a single slit with two lasers?
A single slit with two lasers experiment has various applications in optics and physics. It is commonly used to study the principles of diffraction and interference of light, and can also be applied in the field of spectroscopy to analyze the properties of different materials. Additionally, this setup can be used to calibrate optical instruments and test the accuracy of optical measurements.