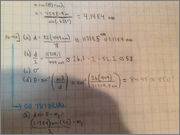Zach Hughes
- 2
- 0
I'm at wits end. I hate WileyPlus. Part A, B and C are correct. I cannot figure out what Part D is -- all of the answers I am getting are wrong.
Double Slit Diffraction:Finding Greatest Angle for Minimum
- Thread starter Zach Hughes
- Start date
Join the discussion
Ask a follow-up here, or get your own question answered by working scientists, mathematicians and engineers — people, not an autocomplete.
Real named experts · corrections over time · the nuance an AI answer skips
1 reply · 1K views
- 15,536
- 1,917
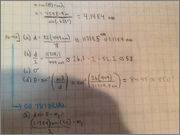
Zach Hughes said:I'm at wits end. I hate WileyPlus. Part A, B and C are correct. I cannot figure out what Part D is -- all of the answers I am getting are wrong.Homework Equations
The Attempt at a Solution
What is the condition for a minimum?