harsh_23
- 5
- 0
- Homework Statement
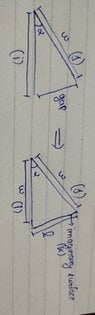
- We need to prove that fraction of total radiation from plate i falling on plate j is equal to 1-sin(α/2) where both plates are infinite long, share a common edge , have same width and are inclined at an angle α
- Relevant Equations
- in general fab represent fraction of total radiation from a falling on b
so sum of all fai =1
The figure is infinite out and in the page.
We need to find $$f_{ij}$$ means if $$I$$ is the total radiation plate i is emitting then $$f_{ij}$$ represent fraction of total radiation Falling on plate $$j$$ from plate $$i$$
$$So in general fab represent fraction of total radiation from a falling on b$$
$$so \ sum \ of \ all\ fai =1$$
So in the above image I want to prove why $$f_{ij} = 1-sin(α/2)$$
First thing I have observed in others proofs that they consider radiation going to the surrounding through the gap between the plates and they consider the gap as an imaginary surface let's call $$k$$ with width l
Now we can see that side l is simply $$2w×sin(α/2)$$
Also $$f_{ki}=f_{kj}=1/2$$
(by symmetry)(means 1/2 of $$k$$ radiation is going to plate $j$ and other to I)
Then by reciprocity theorem
(It's a general theorem in radiation)
(It states that $$A_a×f_{ab}=A_b×f_{ba}$$ (here $$A$$ represent area))
$$A_i×f_{ik}=A_k×f_{ki}$$ (now area of plates is proportional to width)
$$W×f_{ik}=2wsin(α/2)×1/2$$
$$f_{ik}=sin(α/2)$$
And $$f_{ik}+f_{ij}=1$$
So $$f_{ij}=1-sin(α/2)$$
Now my doubt is that radiation shouldn't only be going through the gap but also to the surrounding
So $$f_{ik}+f_{ij}≠1$$
If I call surrounding s then
$$f_{ik}+f_{ij}+f_{is}=1$$
And should be same for all
And even if I don't consider the radiation to surrounding then considering the gap be bit spherical (concave) then some radiation should go to itself so saying
$$f_{ki}=f_{kj}=1/2$$ should be false as some of the total radiation is going to itself.
So someone pls help Clearing My doubt...
Attachments
Last edited: