Doubts about linear elements of electrical circuits

[brunotolentin.4]

First doubt: The impedance Z is defined how Z = R + j X and the reactance X can be wrote how:

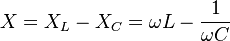
Source: https://en.wikipedia.org/wiki/Electrical_reactance

So, by analogy, the admitance Y is defined how Y = G + j B and the susceptance B can be wrote how what? So:
B = \left( \frac{\omega C}{1} - \frac{1}{\omega L} \right)
Or this form:
B = \left( \frac{1}{\omega L} - \frac{\omega C}{1} \right)
?

Help: https://it.wikipedia.org/wiki/SuscettanzaSecond doubt: in this page: "https://en.wikipedia.org/wiki/Electrical_resistance_and_conductance", the condutance G is defined how the reciprocal of R, BUT, BUT, in this page: "https://en.wikipedia.org/wiki/Susceptance", the condutance G is defined now how:
G = \left( \frac{R}{R^2+X^2} \right)
So, this last equation is the general definition of G and the first definition is the particular case, when X = 0, correct!?

 

[USeptim]

Hi,

About your first question, both forms differ only in the sign and since the reactance is a complex magnitude, the sign is not relevant.

As for your second question, I don't see in https://en.wikipedia.org/wiki/Susceptance the definition of G that you have written.Sergio

 

[brunotolentin.4]

Hi,

About your first question, both forms differ only in the sign and since the reactance is a complex magnitude, the sign is not relevant.

Exist a convention (maybe, can be that exist a good reason for this convention, but I don't know) for the signal of X, if X>0, thus the X is a indutive reactance and if X<0, thus X is capacitive reactance.

So, the duality of the capacitance is the elastance and the duality of the indutance is the relutance. So, by analogy, shoud exist a convention (or a deduction) for the signal of B too. What would be?