Dragstar's maximum acceleration

[cmcd]

Homework Statement

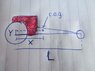
A dragstar which weighs 1000kg has a wheelbase 6m long and is assumed to have an unlimited amount of power available to the rear wheels. If the centre of mass of the vehicle is situated 1m forward of and 0.5m above the contact point of the rear wheels and the coefficient of static friction of the tyre/track interface is 0.6 the maximum acceleration which can be developed before the front wheels lift off is...

A- 3.24m/s^2
B - 9.81m/s^2
C- 19.62m/s^2
D- 5.89m/s^2
E- 7.34m/s^2

http://s1372.photobucket.com/user/cmcdona22/media/002_zps0563b57c.jpg.html?sort=3&o=1
http://s1372.photobucket.com/user/cmcdona22/media/003_zps3253eaf5.jpg.html?sort=3&o=0

Homework Equations

F= ma
F_fric= μR

The Attempt at a Solution

Moments about C.o.G. - horizontal distance x vertical force
2R_A x X =2R_B x ( L - X)
2R_A = 2R_B x (L - X)/X

2R_A + 2R_B = mg

2R_B( 1 + (L - X)/X) = mg
2R_B = [X/L] mg

2R_A = [(L - X)/L] mg

Moment about C.o.G. - vertical distance x horizontal force

M_(about A - The rear wheel) = 0 ... for the car not to lift.


vert force x horiz dist
M_A = 2[(X)/L]mg x (L-X) - 2[(X)/L]m ( a - gμ ) x .5

M_A = 0

a_max = 15.886m/s^2

Am I doing the moments wrong?
Or have I gone wrong elsewhere?
Thanks very much,
cmcd

 

[mfb]

Moments about C.o.G. - horizontal distance x vertical force
2R_A x X =2R_B x ( L - X)

What about vertical distance * horizontal force? The dragster is accelerating.

2R_A + 2R_B = mg

That would make the dragster fly upwards like an airplane.

Where did you use "before the front wheels lift off"? What does that condition mean? Every lower acceleration is possible as well - but there is something special about this point.

M_(about A - The rear wheel) = 0 ... for the car not to lift.

Okay.

vert force x horiz dist
M_A = 2[(X)/L]mg x (L-X) - 2[(X)/L]m ( a - gμ ) x .5

I have no idea what you calculate here.

 

[.Scott]

The coefficient of friction is supplied. How could that value influence the answer?

A warning: Once you calculate the correct answer, you will note that it is either exactly one of the choices they provide or a bit less. If it's a bit less, it's because you took into account the stated fact that only the rear wheels can deliver power but they did not.

 

[cmcd]

@mfb,

The piece where you have no idea what I'm trying to calculate is the vertical distance * horizontal force.

.5 is the vertical distance, Y in the image I attached.

I took the weight at the front wheel to be the reaction force, is that not right?

@.Scott,

Hey .Scott, well it should affect the horizontal force opposite to the motion of the car. And since both wheels experience different reaction forces there's a different amount of friction that they both experience: the rear wheels experience more than the front wheels. The moment about the rear wheels I tried to calculate by multiplying the reaction force at the front wheels by the horizontal distance from the C.o.G. and set it equal to the vertical distance from the C.o.G. by the force due to acceleration.

 

[.Scott]

@.Scott,

Hey .Scott, well it should affect the horizontal force opposite to the motion of the car. And since both wheels experience different reaction forces there's a different amount of friction that they both experience: the rear wheels experience more than the front wheels. The moment about the rear wheels I tried to calculate by multiplying the reaction force at the front wheels by the horizontal distance from the C.o.G. and set it equal to the vertical distance from the C.o.G. by the force due to acceleration.

Let me be more explicit. Given your coefficient of friction, is there any possibility of the front wheels leaving the ground?

 

[mfb]

The piece where you have no idea what I'm trying to calculate is the vertical distance * horizontal force.

Where does your expression for the horizontal force come from?

I took the weight at the front wheel to be the reaction force, is that not right?

Which weight at the front wheel? The equations you have so far are not suitable to get it.